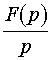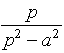BUDAPESTI MŰSZAKI EGYETEM
GÉPÉSZMÉRNÖKI KAR
MATEMATIKA TANSZÉK
a
DIFFERENCIÁLEGYENLETEK ÉS
VEKTORANALÍZIS (T 8)
c. tárgy programja
a BME műszaki menedzser-szak hallgatói számára
A tárgyat előadja: a Gépészkari Matematika Tanszék
a természettudományi blokkban, az 5. szemeszterben,
valamennyi hallgató részére,
4 óra, 4 kredit értékben, vizsga jegy (v) követelménnyel.
Érvényes: 1996 szeptembertől
Készítette: dr. Moson Péter egyetemi docens
Kotsis Domokosné dr. egyetemi adjunktus
Felülvizsgálta: dr. Szántai Tamás egyetemi docens, tanszékvezető helyettes
Jóváhagyta:
1. A tárgy célkitűzése
megismertetni a hallgatóságot a hagyományos differenciálegyenletek és vektoranalízis elmélettel, rövid kitekintéssel a függvénysorok, komplex függvények, Laplace transzformáció kérdéseire. A. műszaki életben felmerülő legfontosabb differenciál-egyenlet típusok megoldása, valamint a differenciálegyenletek egyéb alkalmazásai.
2. A tárgy kapcsolata más tárgyakkal
a tárgy épít a Többváltozós analízis és differenciálegyenletek alapjai (T 2) c. tárgyra, szoros kapcsolatban van, alkalmazásokon keresztül, a Fizika különböző tárgyaival is.
3. A tananyag részletes témakörei
3.1. Közönséges differenciálegyenlet rendszer. Alapfogalmak: integrálgörbe, pályagörbe, a megoldás folytathatósága. Kezdeti-és peremérték feladatok.
3.2. Egzisztencia és unicitás tételek. A kezdeti feltételektől, paraméterektől való folytonos, differenciálható függés.
3.3. Lineáris differenciálegyenlet rendszerek. Lineáris függetlenség, Wronski determináns. A megoldáshalmaz szerkezete. Állandó együtthatós rendszerek. Próbafüggvény módszer. Variációs rendszer.
3.4. n-edrendű differenciálegyenletek. A megoldáshalmaz szerkezete. Az állandók variálásának módszere. Átviteli elv. Nevezetes másodrendű egyenletek (Bessel).
3.5.. Autonóm differenciálegyenlet rendszerek. Pályák, fáziskép. Ljapunov-féle stabilitás, instabilitás, aszimptotikus stabilitás. Stabilitás a lineáris közelítés alapján.
3.6. Vektor-vektor függvények differenciálhatósága. Deriválttenzor és invariánsai (divergencia, rotáció). Másodrendű differenciáloperátorok (Laplace operátor).
3.7. Vektor-vektor függvények vonalmenti integrálja. A vonalintegrál szemléletes jelentése, munka, cirkuláció. Vektor-vektor függvények felületmenti integrálja. Fluxus.
3.8. Integrálátalakító tételek ( Gauss-Osztrogradszkij, Stokes, Green tételek három illetve két dimenzióban, és alkalmazásaik (megmaradási elvek).
3.9. A potenciálelmélet elemei. Potenciálos, konzervatív, örvénymentes vektormezők. Egyszeresen összefüggő tartomány. Harmonikus függvények. Utalás görbevonalu koordinátarendszerekre.
3.10. Függvénysorozatok, sorok pontonkénti, egyenletes, abszolút konvergenciája. Függvénysorozatok, sorok integrálása, differenciálása, a határfüggvány tulajdonságai.
3.11. Hatványsorok, konvergencia sugár. Fourier sorok. Fourier sorfejtés, utalás a különböző konvergencia típusokra.
3.12. Komplex függvénytan alapjai. Deriválás, analitikus függvény. Konformis leképezések.
3.13. Komplex vonalintegrál. Cauchy formula. Residuum tétel.
3.14. Parciális differenciálegyenletek. Problémafelvetés, osztályozás, utalás a főbb megoldási módszerekre. A Fourier módszer. A hővezetés differenciálegyenlete.
3.15. A Laplace transzformáció. Elemi függvények, eltolás, derivált, integrál Laplace transzformáltja. Alkalmazás differenciál és integrálegyenletekre.
4. Ajánlott irodalom
- Farkas Miklós: Matematika VI., VII, VIII.
- Monostory Iván: Matematika Példatár VI., VII, VIII.
- L.Sz. Pontrjagin: Közönséges differenciálegyenletek, Akadémiai Kiadó, 1972.
- V.I. Arnold: Közönséges differenciálegyenletek, Műszaki Könyvkiadó, 1987.
- V.Sz. Vlagyimirov: Bevezetés a parciális differenciálegyenletek elméletébe, Műszaki Könyvkiadó, 1979.
DIFFERENCIÁLEGYENLETEK ÉS
VEKTORANALÍZIS (T 8)
c. tárgy kibővített óravázlata
a BME műszaki menedzser-szak hallgatói számára
készítette
Dr. Moson Péter
egyetemi docens
Budapest, 1996.
1. hét: Közönséges
differenciál-egyenletrendszerek
Közönséges differenciálegyenlet
rendszer. Alapfogalmak: integrálgörbe, pályagörbe, a megoldás folytathatósága. Kezdeti-és peremérték feladatok.
1. Bevezetés. A differenciálegyenletek a folytonos változások (evolúció) leírásának, modellezésének legfontosabb matematikai eszközei. A folyamat jellegétől függően több matematikai elmélet is (közönséges, parciális, retardált, funkcionális differenciálegyenletek stb.) ezen feladat megoldását szolgálja. Egy folyamat közönséges differenciál-egyenletrendszerrel modellezhető, ha rendelkezik (a valóságban természetesen csak valamilyen közelítéssel) az alábbi tulajdonságokkal:
determinisztikus (a múlt és a jövő egyértelműen meghatározható a jelen állapotból)
véges dimenziós (véges sok változóval leírható, az állapottér véges dimenziós)
differenciálható (a leíró függvények símák).
Példaként itt csak az égi mechanika, bolygómozgás kérdéseit említjük (pontszerűnek tekintett Nap illetve bolygók mellett).
Ebben a részben megfogalmazzuk az alapvető kérdéseket, definíciókat, ezek megoldására a 2. hét anyagában térünk ki.
2. A matematikai modell.
A közönséges differenciál-egyenletrendszerek az alábbi matematikai alakban írhatók fel
(1) ![]() , ahol D nyílt, összefüggő,
, ahol D nyílt, összefüggő,![]()
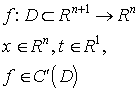
![]() .
.
A rendszert gyakran egy kezdeti érték (más néven Cauchy) problémával együtt tekintjük, azaz
(2) ![]() , ahol
, ahol ![]() .
.
1. Definíció (megoldás). Egy ![]() differenciálható
függvényt az (1) , (2) probléma megoldásának nevezzük, ha teljesül
differenciálható
függvényt az (1) , (2) probléma megoldásának nevezzük, ha teljesül ![]() -ra
-ra ![]() Továbbá
Továbbá ![]() .
.
Látható módon
a megoldás függ az "időtől" (t),
illetve a kezdeti időpillanattól, állapottól ( ![]() ). Amennyiben
explicit módon is jelezni akarjuk az ezen utóbbi változóktól való függőséget,
akkor a függvényt használjuk (argumentuma n+2 dimenziós)
). Amennyiben
explicit módon is jelezni akarjuk az ezen utóbbi változóktól való függőséget,
akkor a függvényt használjuk (argumentuma n+2 dimenziós) ![]() .
.
Az előbbi függvény geometriai szemléltetésénél fontos szerepet játszik az integrálgörbe illetve a pályagörbe fogalma (feltesszük, hogy az (1-2) feladat megoldásai léteznek és egyértelműek).
2. Definíció (integrálgörbe). Integrálgörbének
nevezzük a
grafikonját, az ![]() ponthalmazt.
ponthalmazt.
3. Definíció (pályagörbe). Pályagörbének
nevezzük egy integrálgörbe az állapottérre vett vetületét, azaz ![]() .
.
1.1.példa. Tekintsük
az (1)
, (2) feladatot az ![]() nyilvánvaló esetben.
(Azaz az
nyilvánvaló esetben.
(Azaz az ![]() elsőrendű
differenciálegyenlet kezdeti érték feladatot.) A megoldás világosan egy
exponenciális függvény, a kezdeti értékek figyelembe vételével könnyen
ellenőrizhetően a következő:
elsőrendű
differenciálegyenlet kezdeti érték feladatot.) A megoldás világosan egy
exponenciális függvény, a kezdeti értékek figyelembe vételével könnyen
ellenőrizhetően a következő: ![]() (Ls. 1.1. ábra)
(Ls. 1.1. ábra)
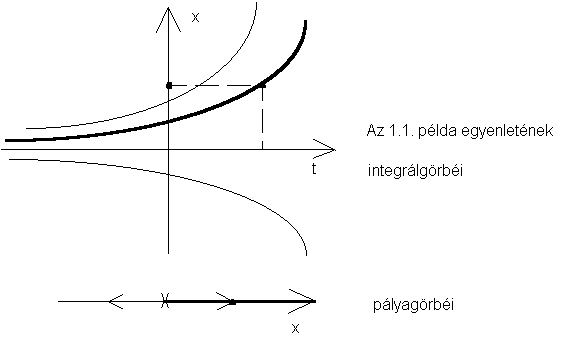 1.1. ábra
1.1. ábra
Az
ábrán a vastagon jelölt vonal az ![]() megoldás
integrál-,illetve pályagörbéje.
megoldás
integrál-,illetve pályagörbéje.
Végezetül megemlítjük, hogy az ![]() intervallumot a megoldás maximális intervallumának (erre utal az
intervallumot a megoldás maximális intervallumának (erre utal az ![]() jelölés) nevezik. A
jelölés is utal arra, hogy a megoldások értelmezési tartománya általában nem az
egész valós számegyenes, hanem egy a kezdeti értéktől (
jelölés) nevezik. A
jelölés is utal arra, hogy a megoldások értelmezési tartománya általában nem az
egész valós számegyenes, hanem egy a kezdeti értéktől (![]() -től) függő nyílt intervallum (ls. 1.2. példa).
-től) függő nyílt intervallum (ls. 1.2. példa).
1.2. példa. Vizsgáljuk az
![]() elsőrendű egyenletet.
A megoldások a tangens függvény és eltoltjai (
elsőrendű egyenletet.
A megoldások a tangens függvény és eltoltjai (![]() ), a maximális intervallum
), a maximális intervallum ![]() . Az egyenlet jobb oldala analitikus, így a probléma nem
simasági jellegű. "Durván " mondva a jelenség lényege, hogy a jobb
oldal túl gyorsan nő, ezért a megoldás véges idő alatt elmegy a végtelenbe.
. Az egyenlet jobb oldala analitikus, így a probléma nem
simasági jellegű. "Durván " mondva a jelenség lényege, hogy a jobb
oldal túl gyorsan nő, ezért a megoldás véges idő alatt elmegy a végtelenbe.
3. Magasabbrendű egyenletek.
A korábbi tanulmányaikban már tárgyalt elsőrendű differenciálegyenletek nyilvánvaló módon speciális esetei az (1-2) összefüggésekkel bevezetett differenciálegyenletrenszereknek. Az alábbiakban megmutatjuk, hogy a magasabbrendű differenciálegyenletek egy egyszerű transzformációval visszavezethetőek diffrenciálegyenletrendszerekre.
Átviteli elv. Az n-edrendű differenciálegyenletek (1'-2') kezdeti érték problémája
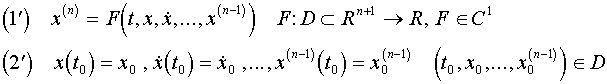
az alábbi transzformációval
![]()
átvihető a vele ekvivalens
![]()
![]()
egyenletrendszer Cauchy problémájába.
1.3 példa. Az ![]() másodrendű egyenlet
(a harmonikus rezgőmozgás egyenlete) az
másodrendű egyenlet
(a harmonikus rezgőmozgás egyenlete) az
![]() transzformáció után
az
transzformáció után
az 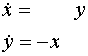 rendszerre vezet.
Ezen rendszerre a pályák origó középpontú koncentrikus körök (és maga az
origó).
rendszerre vezet.
Ezen rendszerre a pályák origó középpontú koncentrikus körök (és maga az
origó).
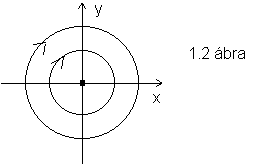 Az
Az 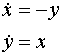 egyenletrendszer
fázisképe.
egyenletrendszer
fázisképe.
2. hét: A
megoldás létezése, kezdeti értékektől való függése.
Egzisztencia és unicitás tételek. A kezdeti feltételektől,
paraméterektől való folytonos, differenciálható függés.
1. Bevezetés. E rész témája az 1. héten
megfogalmazott (1-2) ![]() ,
, ![]() kezdeti
érték probléma megoldása létezésének és egyértelműségének vizsgálata, a kapott
kezdeti
érték probléma megoldása létezésének és egyértelműségének vizsgálata, a kapott ![]() (n+2)
változós függvény vizsgálata.
(n+2)
változós függvény vizsgálata.
2. Ekvivalens integrálegyenlet.
A közönséges differenciálegyenletek elmélete alaptételét, az egzisztencia és unicitás tételt, visszavezetjük egy integrálegyenlet megoldására.
1. lemma. A ![]() ,
, ![]() függvény akkor és csak akkor megoldása
az
függvény akkor és csak akkor megoldása
az
(1-2) ![]() ,
,![]()
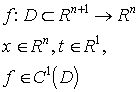 ,
,![]() ,
, ![]()
![]() differenciálegyenlet-rendszernek,
ha megoldása az alábbi integrálegyenletnek
differenciálegyenlet-rendszernek,
ha megoldása az alábbi integrálegyenletnek
(3) 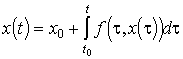 .
.
Bizonyítás. Egyszerűen adódik a differenciálegyenlet mindkét oldala integrálásával, illetve az integrálegyenlet differenciálásával.!
Megjegyzendő,
hogy az integrálegyenlet lehetőséget ad a megoldás közelítésére (Picard-féle
szukcesszív approximációs módszer): Legyen ![]() , tekintsük a rekurzív módon megadott
, tekintsük a rekurzív módon megadott 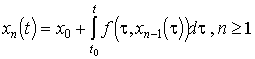 függvénysorozatot.
Igazolható, hogy bizonyos feltételek mellett (ls. egzisztencia és unicitás
tétel) az
függvénysorozatot.
Igazolható, hogy bizonyos feltételek mellett (ls. egzisztencia és unicitás
tétel) az ![]() függvénysorozat
konvergál (1-2) ill. (3)
megoldásához.
függvénysorozat
konvergál (1-2) ill. (3)
megoldásához.
3.A.
KITÉRŐ. Metrikus terek. Kontrakció.
Az előbb említett függvénysorozat konvergenciája pl. bizonyítható egy általánosabb tételből, a metrikus tereken megadott leképezésekre vonatkozó Banach-féle fixpont tételből. Röviden emlékeztetjük az olvasót a legfontosabb definíciókra és megfogalmazzuk a tételt.
1. Definíció. (metrikus tér). Egy X halmazt metrikus térnek nevezünk, ha
adott egy ![]() függvény (metrika -
távolságfüggvény) az alábbi tulajdonságokkal
függvény (metrika -
távolságfüggvény) az alábbi tulajdonságokkal
(i) ![]() ,
,
(ii) ![]() ,
,
(iii) ![]() (háromszög egyenlőtlenség).
(háromszög egyenlőtlenség).
3.1. példa.
A kurzusunkban leggyakrabban használt metrikus terek az ![]() (metrika:
(metrika: 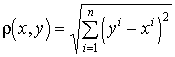 ), illetve a zárt
intervallumon megadott folytonos folytonos függvények tere
), illetve a zárt
intervallumon megadott folytonos folytonos függvények tere ![]() (
( ![]() ).
).
Emlékeztetünk
arra, hogy egy ![]() sorozatot Cauchy
sorozatnak nevezzük, ha
sorozatot Cauchy
sorozatnak nevezzük, ha ![]() . Egy tér teljes, ha abban minden Cauchy sorozat konvergens.
. Egy tér teljes, ha abban minden Cauchy sorozat konvergens.
Tétel (Banach-féle fix pont). Legyen X teljes metrikus tér, ![]() leképezés kontrakció
(
leképezés kontrakció
(![]() olyan, hogy
olyan, hogy ![]() -re
-re ![]() ), akkor az F -nek
létezik egyetlen fix pontja
), akkor az F -nek
létezik egyetlen fix pontja ![]() , és az megkereshető a szukcesszív approximáció
módszerével
, és az megkereshető a szukcesszív approximáció
módszerével 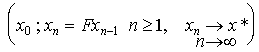 .
.
3.B.
KITÉRŐ. Normált terek. Lipschitz feltétel.
Az (1-2) probléma megoldhatóságához az f függvényre bizonyos simasági
feltételeket kell feltenni. Ezek bevezetése történik itt.
![]() 2. Definíció. (normált tér). Egy X halmazt normált térnek nevezünk, ha adott egy
2. Definíció. (normált tér). Egy X halmazt normált térnek nevezünk, ha adott egy ![]() függvény (norma -
hosszúságfüggvény) az alábbi tulajdonságokkal
függvény (norma -
hosszúságfüggvény) az alábbi tulajdonságokkal
(i) ![]() ,
,
(ii) ![]() ,
,
(iii) ![]()
![]() (háromszög egyenlőtlenség).
(háromszög egyenlőtlenség).
Megjegyzendő,
hogy a norma segítségével megadható egy metrika ![]() .
.
3.2. példa.
A kurzusunkban leggyakrabban használt normált terek az ![]() (
(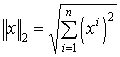 ), illetve a zárt intervallumon megadott folytonos folytonos
függvények tere
), illetve a zárt intervallumon megadott folytonos folytonos
függvények tere ![]() (
( ![]() ), a mátrixok
(lineáris operátorok) normája
), a mátrixok
(lineáris operátorok) normája 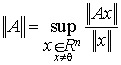 . Ezen utóbbira nyilván igaz az
. Ezen utóbbira nyilván igaz az ![]() egyenlőtlenség.
egyenlőtlenség.
3. Definíció. (Lipschitz feltétel). Azt
mondjuk, hogy az f függvény ![]() kielégíti az x-szerinti Lipschitz feltételt (L állandóval), ha
kielégíti az x-szerinti Lipschitz feltételt (L állandóval), ha ![]() -re
-re ![]() . Amennyiben D minden pontjának van olyan környezete
melyre teljesülnek a fentiek, akkor lokális Lipschitz feltételről beszélünk.
Jelölés:
. Amennyiben D minden pontjának van olyan környezete
melyre teljesülnek a fentiek, akkor lokális Lipschitz feltételről beszélünk.
Jelölés: ![]() . Megjegyezzük, ha f folytonosan
differenciálható D-ben akkor
. Megjegyezzük, ha f folytonosan
differenciálható D-ben akkor ![]() és tetszőleges D-beli kompaktra
és tetszőleges D-beli kompaktra 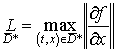 .
.
4. Egzisztencia és unicitástétel.
Tétel. A közönséges differenciálegyenletek (1-2) kezdeti érték problémájának
(1) ![]() ,
,
(2) ![]()
a fenti feltételek mellett létezik és egyértelmű a megoldása.
Megjegyzések.
- A tétel feltételei ( f folytonos és Lipschitz-es) elégségesek a megoldás létezéséhez és egyértelműségéhez, de nem szükségesek. A 3.B. megjegyzéséből (az f folytonosan deriválható) egy erősebb, de könnyebben ellenőrizhető elégséges feltétel adódik.
- A megoldás létezését a tétel lokálisan, a ![]() pont egy
környezetében garantálja.
pont egy
környezetében garantálja.
- A tétel bizonyítható úgy, hogy az 1.lemma integrálegyenlete megoldása létezését és egyértelműségét igazoljuk a Banach-féle fixpont tétel segítségével.
- A megoldás
és annak értelmezési tartománya függ a kezdeti értéktől. Ezt az ![]() illetve a
illetve a ![]() jelölésekkel fejezzük
ki.
jelölésekkel fejezzük
ki.
5. A kezdeti értékektől való függés.
Tétel. Ha az (1-2) kezdeti érték
probléma esetén ![]() , akkor a
, akkor a ![]() (n+2) változós
függvény folytonosan differenciálható minden argumentumában.
(n+2) változós
függvény folytonosan differenciálható minden argumentumában.
Megjegyzések.
- Ha f analitikus, akkor a megoldás is analitikus lesz.
- Az előbbi tétel igaz akkor is, ha f függ egy (általában m változós) paramétertől.
- A megoldásfüggvény kezdeti érték, illetve paraméter szerinti deriváltjainak kiszámítására a 3. hét anyagában térünk ki, mivel ezek egy lineáris egyenletrendszer (a variációs rendszer) megoldására vezetnek. Ott utalunk majd a deriváltak alkalmazhatóságára, szemléletes jelentésére.
3. hét: Lineáris differenciálegyenlet rendszerek.
Lineáris differenciálegyenlet rendszerek.
Lineáris függetlenség, Wronski determináns. A megoldáshalmaz szerkezete.
Állandó együtthatós rendszerek. Próbafüggvény módszer. Variációs rendszer.
1. Bevezetés.
Az 1-2. heteken tárgyalt általános alakú közönséges rendszerek megoldása létezik az adott feltételek mellett, de nem kereshető meg általában elemi módszerekkel. Ezért, illetőleg az alkalmazásokban való gyakori fellépésük miatt, a továbbiakban speciális alakú rendszerek vizsgálatára térünk át. Lineárisnak nevezünk egy rendszert, ha a jobb oldal a függő változóban legfeljebb elsőfokú. Amennyiben vannak 0. fokú tagok, akkor inhomogén lineáris változó-együtthatós egyenletrendszernek nevezzük az alábbit
![]() ,
,
ahol A (n*n)-es
mátrix, b (n*1)-es oszlopvektor ugyanazon az intervallumon megadott
folytonos függvény elemekkel. A ![]() tartomány tetszőleges
pontját kezdeti értékként véve a megfelelő Cauchy problémának létezik és
egyértelmű a megoldása (mivel az egzisztencia és unicitás tétel feltételei
nyilvánvalóan teljesülnek). Igazolható továbbá, hogy minden megoldás
értelmezési tartománya (maximális intervalluma) az egész
tartomány tetszőleges
pontját kezdeti értékként véve a megfelelő Cauchy problémának létezik és
egyértelmű a megoldása (mivel az egzisztencia és unicitás tétel feltételei
nyilvánvalóan teljesülnek). Igazolható továbbá, hogy minden megoldás
értelmezési tartománya (maximális intervalluma) az egész ![]() időintervallum. A
továbbiakban röviden ismertetjük a lineáris rendszerek megoldása struktúrájára
vonatkozó eredményeket.
időintervallum. A
továbbiakban röviden ismertetjük a lineáris rendszerek megoldása struktúrájára
vonatkozó eredményeket.
2. Homogén rendszer.
Ha egy lineáris rendszerben a jobb oldalon csak elsőfokú tagok vannak a független változóban, akkor homogén rendszerről beszélünk
![]() .
.
Definíció (vektor függvények lineáris függetlensége).
Az ![]() függvényeket
lineárisan függetlennek nevezzük, ha
függvényeket
lineárisan függetlennek nevezzük, ha ![]() esetén.
esetén.
1. állítás. Ha ![]() megoldása (H)-nak,
akkor lineáris kombinációjuk
megoldása (H)-nak,
akkor lineáris kombinációjuk ![]() is megoldás.
is megoldás.
2. állítás. A ![]() megoldásai (H)-nak
akkor és csak akkor lineárisan függetlenek, ha a belőlük képzett Wronski
determináns -
megoldásai (H)-nak
akkor és csak akkor lineárisan függetlenek, ha a belőlük képzett Wronski
determináns - ![]() - értéke nem egyenlő nullával.
- értéke nem egyenlő nullával.
Megjegyzés
(Liouville tétele). Ha ![]() megoldásai (H)-nak
akkor
megoldásai (H)-nak
akkor 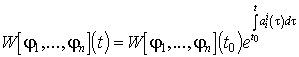 , ahol
, ahol 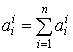 a rendszer mátrixának
nyoma, azaz a fődiagonálisában álló elemek összege.
a rendszer mátrixának
nyoma, azaz a fődiagonálisában álló elemek összege.
3. állítás (Általános megoldás). Ha a (H) rendszer ![]() megoldásai lineárisan
függetlenek, akkor a (H) általános
megoldása
megoldásai lineárisan
függetlenek, akkor a (H) általános
megoldása ![]() alakú.
alakú.
Elnevezések.
A ![]() lineárisan független
megoldásokat alaprendszernek, a
belőlük képezett
lineárisan független
megoldásokat alaprendszernek, a
belőlük képezett ![]() mátrixot alapmátrixnak nevezzük.
mátrixot alapmátrixnak nevezzük.
Az alapmátrix
segítségével az általános megoldás felírása a következő (mátrixos) alakot
ölti ![]() , ahol
, ahol ![]()
![]() .
.
Megjegyezzük továbbá, ha a (H) rendszernek ismert k lineárisan független megoldása, akkor a rendszer visszavezethető egy n-k dimenziós rendszerre.
3. Inhomogén rendszer.
Struktúra tétel. Az ![]() inhomogén rendszer
általános megoldása
inhomogén rendszer
általános megoldása ![]() alakú, ahol
alakú, ahol ![]() a homogén rendszer
általános megoldása,
a homogén rendszer
általános megoldása, ![]() pedig az inhomogén
rendszer egy partikuláris megoldása.
pedig az inhomogén
rendszer egy partikuláris megoldása.
1.Megjegyzés.
Egy ![]() partikuláris
megoldásnak vehető például az
partikuláris
megoldásnak vehető például az 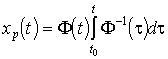 függvény. Ezen
összefüggésekből jól látható, hogy az n dimenziós
rendszerre kapott eredmények összhangban vannak a korábbi
differenciálegyenletek tanulmányokban (T2 kurzus) megismert lineáris
egyenletekkel. Az
függvény. Ezen
összefüggésekből jól látható, hogy az n dimenziós
rendszerre kapott eredmények összhangban vannak a korábbi
differenciálegyenletek tanulmányokban (T2 kurzus) megismert lineáris
egyenletekkel. Az ![]() egyenlet általános
megoldása ugyanezt a struktúrát (homogén általános megoldása + egy partikuláris
megoldás) követi
egyenlet általános
megoldása ugyanezt a struktúrát (homogén általános megoldása + egy partikuláris
megoldás) követi ![]() .
.
2.Megjegyzés.
(szuperpozíció elv). Ha ![]() , akkor az
, akkor az ![]() rendszer egy
partikuláris megoldásához hozzáadva az
rendszer egy
partikuláris megoldásához hozzáadva az ![]() egy partikuláris
megoldását az eredeti (IH) rendszer
partikuláris megoldását kapjuk, azaz
egy partikuláris
megoldását az eredeti (IH) rendszer
partikuláris megoldását kapjuk, azaz ![]() .
.
4. Állandó együtthatós rendszerek.
Az (IH) rendszert állandó együtthatósnak nevezzük, ha az A mátrix elemei állandók (konstans függvények). A b oszlopvektor elemei megmaradnak függvényeknek. Ebben a speciális esetben még jobban látszik az analógia az előbb idézett lineáris egyenlettel, ugyanis a megoldás exponenciális függvény alakú marad.
1. állítás. A ![]() állandó együtthatós
inhomogén rendszer általános megoldása felírható az alábbi alakban
állandó együtthatós
inhomogén rendszer általános megoldása felírható az alábbi alakban ![]() .
.
Megjegyzés.
Az előbbi formulában szereplő ![]() alapmátrix
számítására több módszer létezik. Ha az A
mátrix
alapmátrix
számítására több módszer létezik. Ha az A
mátrix ![]() sajátértékei
különbözők, akkor
sajátértékei
különbözők, akkor ![]() , ahol az
, ahol az ![]() vektorok a
vektorok a ![]() sajátértékeknek
megfelelő sajátvektorok. (Ha el akarjuk kerülni komplex kifejezések
megjelenését az általános megoldásunkban, akkor pl. ha
sajátértékeknek
megfelelő sajátvektorok. (Ha el akarjuk kerülni komplex kifejezések
megjelenését az általános megoldásunkban, akkor pl. ha ![]() egy komplex konjugált
gyökpár, a nekik megfelelő két lineárisan független megoldásoknak vehető
az
egy komplex konjugált
gyökpár, a nekik megfelelő két lineárisan független megoldásoknak vehető
az ![]() vektorfüggvény valós
illetve képzetes része.)
vektorfüggvény valós
illetve képzetes része.)
Az inhomogén
állandó-együtthatós rendszerek partikuláris megoldása az 1. állításban szereplő
integrálnál lényegesen egyszerűbben meghatározható, ha a b oszlopvektor elemei polinomiális, exponenciális, trigonometrikus
függvények, vagyis 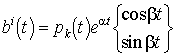 . A szuperpozíció elv
szerint nyilván lehetséges külön-külön megkeresni a partikuláris megoldásokat
az ilyen alakú tagokra, majd ezeket összeadni.
. A szuperpozíció elv
szerint nyilván lehetséges külön-külön megkeresni a partikuláris megoldásokat
az ilyen alakú tagokra, majd ezeket összeadni.
2. állítás (próbafüggvény módszer).
Tekintsük az ![]() inhomogén állandó
együtthatós rendszert, ahol
inhomogén állandó
együtthatós rendszert, ahol 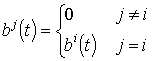 ,
, 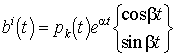 , legyenek az A mátrix sajátértékei
, legyenek az A mátrix sajátértékei ![]() , legyen
, legyen ![]() .
.
a).
nem-rezonáns eset ( ![]() ). Létezik olyan
). Létezik olyan ![]() partikuláris megoldás
vektor, mely minden eleme a
partikuláris megoldás
vektor, mely minden eleme a ![]() -vel megegyező alakú polinomiális, exponenciális,
trigonometrikus függvény. (a k. fokú polinom együtthatóit a határozatlan
együtthatók módszerével, behelyettesítéssel lehet megkeresni)
-vel megegyező alakú polinomiális, exponenciális,
trigonometrikus függvény. (a k. fokú polinom együtthatóit a határozatlan
együtthatók módszerével, behelyettesítéssel lehet megkeresni)
a). rezonáns eset ( ![]() ). Létezik olyan
). Létezik olyan ![]() partikuláris megoldás
vektor, mely minden eleme a
partikuláris megoldás
vektor, mely minden eleme a ![]() -vel megegyező alakú polinomiális, exponenciális,
trigonometrikus függvény, csak a k. fokú polinomok helyett k+l. fokúkat kell tekinteni (l
multiplicitása a karakterisztikus egyenlet
gyökei (az A mátrix sajátértékei között).
-vel megegyező alakú polinomiális, exponenciális,
trigonometrikus függvény, csak a k. fokú polinomok helyett k+l. fokúkat kell tekinteni (l
multiplicitása a karakterisztikus egyenlet
gyökei (az A mátrix sajátértékei között).
5. Variációs rendszer.
A lineáris rendszerek eddigi tárgyalásából látszik, hogy az állandó együtthatósak mindig megoldhatók elemi módszerekkel, a változó együtthatósak kezelése is lényegesen egyszerűbb az általános alakú differenciál-egyenletrendszerekénél. Többek között evvel is magyarázható, hogy az alkalmazásokban fontos szerepet játszik a linearizálás módszere. A problémafelvetés a következő:
A 2. hét 5. A
kezdeti értékektől való függés pontjában megfogalmaztuk,hogy a (1-2)
![]() ,
, ![]() kezdeti érték
problémákat megoldó
kezdeti érték
problémákat megoldó ![]() (n+2) változós
függvény folytonosan differenciálható minden argumentumában. Felmerül a kérdés,
hogy mennyivel egyenlőek az így kapott függvény parciális
deriváltjai. A t szerinti derivált
nyilvánvalóan adódik a megoldás definíciójából. Az
(n+2) változós
függvény folytonosan differenciálható minden argumentumában. Felmerül a kérdés,
hogy mennyivel egyenlőek az így kapott függvény parciális
deriváltjai. A t szerinti derivált
nyilvánvalóan adódik a megoldás definíciójából. Az ![]() (kezdeti érték
szerinti) parciális derivált kielégíti az alábbi összefüggést
(kezdeti érték
szerinti) parciális derivált kielégíti az alábbi összefüggést 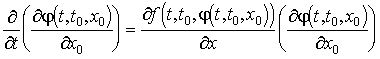 , és igaz a
, és igaz a
Tétel. A ![]() függvény
függvény ![]() szerinti deriváltja
szerinti deriváltja 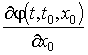 megoldása a (3) lineáris
differenciál-egyenletrendszer
megoldása a (3) lineáris
differenciál-egyenletrendszer
(3) 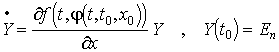 kezdeti érték
problémájának (
kezdeti érték
problémájának (![]() itt az n*n-es egységmátrixot jelöli).
itt az n*n-es egységmátrixot jelöli).
Elnevezés. A (3) homogén lineáris rendszert az (1-2) rendszer megoldásra vonatkozó variációs rendszerének nevezik.
A kapott
eredmény felhasználhatóságát mutatja, ha a
megoldást az ![]() pont környezetében
Taylor sorba fejtjük (vagyis az érdekel bennünket, mi történik ha az adott
pont környezetében
Taylor sorba fejtjük (vagyis az érdekel bennünket, mi történik ha az adott ![]() kezdeti értéktől
kissé eltérő x kezdeti értékkel indul
megoldásunk)
kezdeti értéktől
kissé eltérő x kezdeti értékkel indul
megoldásunk) 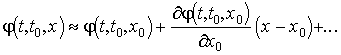 .
.
6. Paraméterektől való függés.
A gyakorlatban fellépő differenciál-egyenletrendszerek megoldásai nemcsak az időtől, a kezdeti időpillanattól és értéktől, de bizonyos paraméterektől is függhetnek. Tekintsük a
(4) ![]()
![]() paraméterektől () függő rendszert.
paraméterektől () függő rendszert.
Tétel. A (4) rendszer ![]() megoldása minden
változójában folytonosan differenciálható és a koordinátái szerinti
deriváltakra igaz
megoldása minden
változójában folytonosan differenciálható és a koordinátái szerinti
deriváltakra igaz 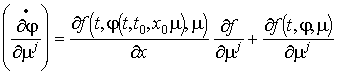 , vagyis
, vagyis ![]() kielégíti az (5) inhomogén lineáris variációs
rendszer Cauchy problémáját
kielégíti az (5) inhomogén lineáris variációs
rendszer Cauchy problémáját
(5) 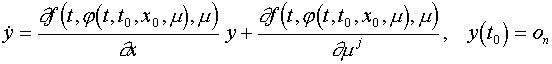 , ahol
, ahol ![]() n*1-es oszlopvektor 0 elemekkel.
n*1-es oszlopvektor 0 elemekkel.
A paraméter szerinti deriváltak a kezdeti érték szerintiekhez hasonlóan használhatóak.
4. hét: n-edrendű
lineáris differenciálegyenletek.
A
megoldáshalmaz szerkezete. Az állandók variálásának módszere. Átviteli elv.
Nevezetes másodrendű egyenletek (Bessel).
Elnevezés. Az n-edrendű lineáris differenciálegyenlet kezdeti kezdeti érték problémájának nevezzük az alábbit
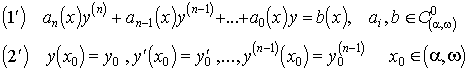 .
.
Az 1. téma, 3. Magasabbrendű egyenletek, Átviteli elv részéhez hasonlóan az n-edrendű lineáris differenciálegyenletek (1'-2') kezdeti érték problémája az alábbi transzformációval
![]()
átvihető a vele ekvivalens
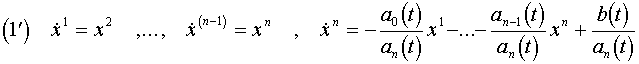
![]()
lineáris
változó együtthatós inhomogén egyenletrendszer Cauchy problémájába. Feltéve,
hogy ![]() , a 3. hét. Lineáris differenciálegyenlet rendszerek,
Bevezetésben tárgyaltakból következik az
y
megoldás létezése és n-szeres differenciálhatósága az
egész (,) intervallumon. Elvben az egyenleteket
így visszavezetve rendszerekre a tárgyalást itt be is lehetne fejezni. A
gyakorlatban azonban sokszor lépnek fel egyenletek (ls. pl. a Newton-i
mechanika másodrendű egyenletei), ezért röviden összefoglaljuk az ezen esetre
vonatkozó specialitásokat.
, a 3. hét. Lineáris differenciálegyenlet rendszerek,
Bevezetésben tárgyaltakból következik az
y
megoldás létezése és n-szeres differenciálhatósága az
egész (,) intervallumon. Elvben az egyenleteket
így visszavezetve rendszerekre a tárgyalást itt be is lehetne fejezni. A
gyakorlatban azonban sokszor lépnek fel egyenletek (ls. pl. a Newton-i
mechanika másodrendű egyenletei), ezért röviden összefoglaljuk az ezen esetre
vonatkozó specialitásokat.
2. Homogén egyenlet.
Ha egy lineáris egyenletben a jobb oldalon levő függvény azonosan 0, akkor homogén egyenletről beszélünk
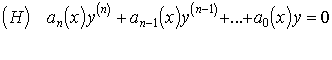 .
.
Definíció (függvények lineáris függetlensége).
Az ![]() függvényeket
lineárisan függetlennek nevezzük, ha
függvényeket
lineárisan függetlennek nevezzük, ha ![]() esetén.
esetén.
1. állítás. Ha ![]() megoldása (H)-nak,
akkor lineáris kombinációjuk
megoldása (H)-nak,
akkor lineáris kombinációjuk ![]() is megoldás.
is megoldás.
2. állítás. A ![]() megoldásai (H)-nak
akkor és csak akkor lineárisan függetlenek, ha a belőlük képzett Wronski
determináns -
megoldásai (H)-nak
akkor és csak akkor lineárisan függetlenek, ha a belőlük képzett Wronski
determináns - 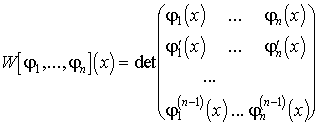 - értéke nem egyenlő nullával.
- értéke nem egyenlő nullával.
Megjegyzés
(Liouville tétele). Ha ![]() megoldásai (H)-nak
akkor
megoldásai (H)-nak
akkor 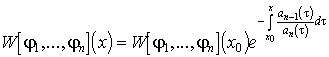 . A megjegyzés helyessége könnyen látszik az átviteli elvvel
kapott mátrixból, hiszen annak nyoma
. A megjegyzés helyessége könnyen látszik az átviteli elvvel
kapott mátrixból, hiszen annak nyoma 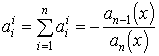 .
.
3. állítás (Általános megoldás). Ha a (H) rendszer ![]() megoldásai lineárisan
függetlenek, akkor a (H) általános
megoldása
megoldásai lineárisan
függetlenek, akkor a (H) általános
megoldása ![]() alakú.
alakú.
Itt is igaz a megjegyzés, ha a (H) egyenletnek ismert k lineárisan független megoldása, akkor az egyenlet visszavezethető egy n-k dimenziós egyenletre.
3. Inhomogén egyenlet.
Struktúra tétel. Az ![]() inhomogén egyenlet általános
megoldása
inhomogén egyenlet általános
megoldása ![]() alakú, ahol
alakú, ahol ![]() a homogén egyenlet
általános megoldása,
a homogén egyenlet
általános megoldása, ![]() pedig az inhomogén
rendszer egy partikuláris megoldása.
pedig az inhomogén
rendszer egy partikuláris megoldása.
1.Megjegyzés
(az állandók variálása). Ezt a módszert másodrendű egyenletekre mutatjuk be (n=2). Egy ![]() partikuláris megoldás
kereshető
partikuláris megoldás
kereshető ![]() alakban (
alakban ( ![]() a homogén egyenlet két lineárisan független megoldása). Az
a homogén egyenlet két lineárisan független megoldása). Az ![]() megoldás
behelyettesítése az (IH) egyenletbe a
következő lineáris algebrai
egyenletrendszert adja
megoldás
behelyettesítése az (IH) egyenletbe a
következő lineáris algebrai
egyenletrendszert adja
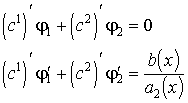 .
.
Innen ![]() mindig egyértelműen
meghatározható, mivel a rendszer determinánsa éppen a Wronski determináns, ami
lineárisan független megoldások esetén nem 0.
mindig egyértelműen
meghatározható, mivel a rendszer determinánsa éppen a Wronski determináns, ami
lineárisan független megoldások esetén nem 0. ![]() -ből már integrálással adódik
-ből már integrálással adódik ![]() és így az
és így az ![]() partikuláris
megoldás.
partikuláris
megoldás.
Látható, hogy mind a rendszerekre, mind az egyenletekre a homogén feladat megoldásának ismerete már egy integrálás után mindig megadja az inhomogén megoldását is. Megjegyezzük újra viszont, hogy nincs általános módszer a homogén feladat n lineárisan független megoldása meghatározására.
2.Megjegyzés.
(szuperpozíció elv). Ha ![]() , akkor az
, akkor az ![]() egyenlet egy
partikuláris megoldásához hozzáadva az
egyenlet egy
partikuláris megoldásához hozzáadva az ![]() egy partikuláris
megoldását az eredeti (IH) egyenlet
partikuláris megoldását kapjuk, azaz
egy partikuláris
megoldását az eredeti (IH) egyenlet
partikuláris megoldását kapjuk, azaz ![]() .
.
4. Állandó együtthatós egyenletek.
Az (IH)
egyenletet állandó együtthatósnak nevezzük, ha ![]() -k állandók (konstans függvények). A b megmaradhat függvénynek. Ebben a
speciális esetben a homogén egyenlet általános megoldásának meghatározása egy
algebrai egyenletre (az un. karakterisztikus egyenletre) vezet, és így elvben
mindig megoldható.
-k állandók (konstans függvények). A b megmaradhat függvénynek. Ebben a
speciális esetben a homogén egyenlet általános megoldásának meghatározása egy
algebrai egyenletre (az un. karakterisztikus egyenletre) vezet, és így elvben
mindig megoldható.
1. állítás. A ![]() állandó együtthatós
homogén egyenlet általános megoldása felírható az
állandó együtthatós
homogén egyenlet általános megoldása felírható az ![]() alakban, ahol
alakban, ahol ![]() az
az ![]() karakterisztikus
egyenlet gyökei (feltéve, hogy azok különbözőek és valósak).
karakterisztikus
egyenlet gyökei (feltéve, hogy azok különbözőek és valósak).
Megjegyzések.
1.
Ha többszörös valós gyök (legyen a multiplicitása k), akkor az ezen által generált k darab lineárisan független megoldás a
következő ![]() .
.
2.
Komplex gyökök esetén a lineárisan független megoldások választhatók valósnak
(mivel az együtthatók valósak). Ha ![]() , akkor
, akkor ![]() ,
, ![]()
Az inhomogén
állandó-együtthatós egyenletek partikuláris megoldása az 3.1. megjegyzésben
szereplő állandók variálása módszernél lényegesen egyszerűbben meghatározható,
ha a b függvény polinomiális,
exponenciális, trigonometrikus , vagyis
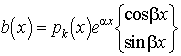 . A szuperpozíció elv
szerint nyilván lehetséges külön-külön megkeresni a partikuláris megoldásokat
az ilyen alakú tagokra, majd ezeket összeadni.
. A szuperpozíció elv
szerint nyilván lehetséges külön-külön megkeresni a partikuláris megoldásokat
az ilyen alakú tagokra, majd ezeket összeadni.
2. állítás (próbafüggvény módszer).
Tekintsük az ![]() inhomogén állandó
együtthatós egyenletet, ahol
inhomogén állandó
együtthatós egyenletet, ahol 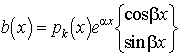 , legyenek
, legyenek ![]() az
az ![]() karakterisztikus
egyenlet gyökei , legyen
karakterisztikus
egyenlet gyökei , legyen ![]() .
.
a).
nem-rezonáns eset ( ![]() ). Létezik olyan
). Létezik olyan ![]() partikuláris
megoldás, mely minden eleme a
partikuláris
megoldás, mely minden eleme a ![]() -el megegyező alakú polinomiális, exponenciális,
trigonometrikus függvény. (a k. fokú polinom együtthatóit a határozatlan
együtthatók módszerével, behelyettesítéssel lehet megkeresni)
-el megegyező alakú polinomiális, exponenciális,
trigonometrikus függvény. (a k. fokú polinom együtthatóit a határozatlan
együtthatók módszerével, behelyettesítéssel lehet megkeresni)
a). rezonáns eset ( ![]() ). Létezik
). Létezik ![]() alakú partikuláris
megoldás (a k. fokú polinomok együtthatóit a határozatlan együtthatók
módszerével, behelyettesítéssel lehet megkeresni itt is).
alakú partikuláris
megoldás (a k. fokú polinomok együtthatóit a határozatlan együtthatók
módszerével, behelyettesítéssel lehet megkeresni itt is).
5. Speciális változó együtthatós lineáris
egyenletek.
Az alkalmazásokban egyes lineáris egyenletek gyakrabban lépnek fel, így ezek megoldására külön elméletek születtek. Itt csak két egyenletet említünk meg.
Euler
egyenletnek nevezzük az ![]() alakú egyenletet,
mely az
alakú egyenletet,
mely az ![]() alakú
helyettesítéssel visszavezethető állandó együtthatós egyenletre.
alakú
helyettesítéssel visszavezethető állandó együtthatós egyenletre.
Bessel
egyenletnek nevezzük az ![]() alakú homogén
lineáris másodrendű egyenletet ( a
alakú homogén
lineáris másodrendű egyenletet ( a ![]() paraméter az egyenlet indexe). a
hengerszimmetriával rendelkező feladatok gyakran vezetnek erre a típusra. A
Bessel egyenletnek megoldásai az
paraméter az egyenlet indexe). a
hengerszimmetriával rendelkező feladatok gyakran vezetnek erre a típusra. A
Bessel egyenletnek megoldásai az 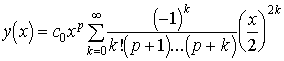 függvények. p=n természetes
szám esetén elsőfajú n-indexű
Bessel-függvénynek nevezzük a
függvények. p=n természetes
szám esetén elsőfajú n-indexű
Bessel-függvénynek nevezzük a ![]() választásnál adódó
választásnál adódó 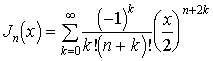 függvényt. A Bessel
függvények több érdekes tulajdonsággal rendelkeznek, amiket itt most nem
részletezünk.
függvényt. A Bessel
függvények több érdekes tulajdonsággal rendelkeznek, amiket itt most nem
részletezünk.
5. hét: Autonóm
differenciál-egyenletrendszerek.
Autonóm differenciálegyenlet
rendszerek. Pályák, fáziskép. Ljapunov-féle stabilitás, instabilitás,
aszimptotikus stabilitás. Stabilitás a lineáris közelítés alapján.
1. Autonóm rendszerek. Egy közönséges differenciál-egyenletrendszert autonómnak nevezünk, ha jobb oldala nem függ explicit módon az időtől (azaz a t változótól). Tekintsük az
![]()
autonóm
rendszert. Az egzisztencia és unicitástétel feltételei teljesülnek, így az ![]() tér tetszőleges
pontját kezdeti értéknek választva létezik megoldás (geometriailag az adott
ponton át megy egy és csak egy integrálgörbe). Az autonóm rendszerek
legfontosabb tulajdonsága, hogy nemcsak az integrálgörbék, de a rendszer pályái
se metszik egymást. A kezdeti értékektől függő megoldásban ( függvény) a kezdeti időpillanatot (
tér tetszőleges
pontját kezdeti értéknek választva létezik megoldás (geometriailag az adott
ponton át megy egy és csak egy integrálgörbe). Az autonóm rendszerek
legfontosabb tulajdonsága, hogy nemcsak az integrálgörbék, de a rendszer pályái
se metszik egymást. A kezdeti értékektől függő megoldásban ( függvény) a kezdeti időpillanatot (![]() ) nullának választva kapjuk az
) nullának választva kapjuk az
![]() függvényt. Az újonnan
definiált függvény segítségével felírható a p ponton átmenő pálya
függvényt. Az újonnan
definiált függvény segítségével felírható a p ponton átmenő pálya
![]() .
.
Egy autonóm rendszer pályái 3 csoportba oszthatók:
egyensúlyi helyzet (stacionárius
pont) a pálya, ha ![]() . Az egyensúlyi
helyzetek az
. Az egyensúlyi
helyzetek az ![]() egyenlet megoldásából
adódnak.
egyenlet megoldásából
adódnak.
zárt pálya (ciklus) a
periodikus megoldásoknak felel meg, azaz
![]() zárt, ha
zárt, ha ![]() , ahol T a megoldás periódusa.
, ahol T a megoldás periódusa.
nem zárt pálya az, amelyik nem esik az előbbi két osztály egyikébe se.
2. Pályák, fáziskép. Egy autonóm rendszer viselkedéséről sok információt nyerhetünk, ha ismerjük a pályáit és a mozgás irányát rajtuk. Fázisképnek nevezzük azokat az ábrákat, melyeken az tartományban berajzoljuk az autonóm rendszer néhány jellemző pályáját (ilyen fázisképeket közöltünk az 1. hét 1.1. illetve 1.3. példájában). A fáziskép meghatározása viszonylag könnyen történik az alacsony dimenziós rendszerekre (n<3), illetve az egyensúlyi helyzetek környékére. A továbbiakban röviden ismertetjük a síkon tekintett (n=2) lineáris autonóm rendszerek egyensúlyi helyzetei közelében fellépő legegyszerűbb fázisképeket.
Feltételezzük, hogy az egyensúlyi helyzet az origó, azaz a (0,0) pont. A vizsgált lineáris rendszer
![]()
alakú, ahol a,b,c,d valós állandók. Írjuk fel a rendszerünket mátrixos alakban
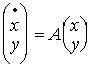 ,
, ![]() .
.
Legyenek , az A mátrix
sajátértékei. Tegyük fel, hogy ![]() . Ekkor a következő fázisképek lehetségesek
. Ekkor a következő fázisképek lehetségesek
csomópont, ha , valósak és azonos előjelűek.
Ekkor a pályák: az origó, a , sajátértékeknek megfelelő sajátvektorok félegyenesei (irányítás
az origó felé, ha , negatívak, az origótól el, ha , pozitívak), a többi pálya "parabolaszerűen" érinti az
egyik sajátvektor félegyenenesét (pl. a -ét, ha ![]() ).
).
nyeregpont, ha , valósak és ellentétes előjelűek. Ekkor a pályák: az origó, a , sajátértékeknek megfelelő sajátvektorok félegyenesei (irányítás <0-ra az origó felé, >0-ra origótól el), a többi pálya "hiperbolaszerűen" érinti a sajátvektorok félegyeneneseit.
fókuszpont, ha ![]() konjugált komplex
sajátértékek és a valós részük nem nulla. Ekkor a pályák: az origó, továbbá az
origóra "spirálisan" rácsavarodó (ha a gyökök valós része negatív,
konjugált komplex
sajátértékek és a valós részük nem nulla. Ekkor a pályák: az origó, továbbá az
origóra "spirálisan" rácsavarodó (ha a gyökök valós része negatív, ![]() ),
"spirálisan" lecsavarodó (ha a gyökök valós része pozitív) nemzárt
pályák..
),
"spirálisan" lecsavarodó (ha a gyökök valós része pozitív) nemzárt
pályák..
centrum, ha ![]() konjugált komplex sajátértékek
és a valós részük nulla,
konjugált komplex sajátértékek
és a valós részük nulla, ![]() . Ekkor a pályák: az origó, továbbá az origót körülvevő zárt
pályák.
. Ekkor a pályák: az origó, továbbá az origót körülvevő zárt
pályák.
3. Ljapunov-féle stabilitás, instabilitás,
aszimptotikus stabilitás. A differenciálegyenletek vizsgálatánál gyakran
elegendő arra a kérdésre válaszolni, hogy mi történik a rendszer megoldásaival
hosszú idő elmúltával, vagyis a ![]() esetben. Evvel a
témakörrel foglalkozik a differenciálegyenletek stabilitáselmélete. Itt most
csak autonóm rendszerek egyensúlyi helyzeteit, abból a szempontból , ha
ugyanabban az időpillanatban "közeli" kezdeti értékű pontokból
elindítunk megoldásokat, akkor azok
esetben. Evvel a
témakörrel foglalkozik a differenciálegyenletek stabilitáselmélete. Itt most
csak autonóm rendszerek egyensúlyi helyzeteit, abból a szempontból , ha
ugyanabban az időpillanatban "közeli" kezdeti értékű pontokból
elindítunk megoldásokat, akkor azok ![]() esetén is közel
maradnak-e az egyensúlyi helyzetünkhöz. Ez a Ljapunov-féle stabilitás
problémaköre. Pontosabban, tekintsük az
esetén is közel
maradnak-e az egyensúlyi helyzetünkhöz. Ez a Ljapunov-féle stabilitás
problémaköre. Pontosabban, tekintsük az
![]()
autonóm
rendszert. A fenti feltételekből következik, hogy az origó (x=0) megoldás. Tegyük fel továbbá, hogy
minden megoldás értelmezési tartománya az egész számegyenes ( ![]() ).
).
1. Definíció. (Ljapunov stabilitás). Az (1') rendszer x=0 megoldását Ljapunov értelemben stabilisnek nevezzük, ha
![]() .
.
Instabilitás alatt az előbbi definíció tagadását értjük, azaz
2. Definíció. (Ljapunov instabilitás). Az (1') rendszer x=0 megoldását Ljapunov értelemben instabilisnek nevezzük, ha
![]() .
.
Az origó
Ljapunov stabilitása azt garantálja, hogy a közeléből induló megoldások nem
távolodnak el az idő múlásával. Ha ezen megoldások még ![]() -re tartanak az origóhoz, akkor aszimptotikus stabilitásról
beszélünk.
-re tartanak az origóhoz, akkor aszimptotikus stabilitásról
beszélünk.
3. Definíció. (Ljapunov aszimptotikus stabilitás). Az (1') rendszer x=0 megoldását Ljapunov értelemben aszimptotikusan stabilisnek nevezzük, ha
(i) az x=0 megoldás Ljapunov stabilis, vagyis
![]() ,
,
(ii) ![]() .
.
A fenti stabilitási fogalmak vizsgálata történhet az un. Ljapunov-féle függvények segítségével. Erre itt nem térünk ki, csak egy fontos következményt tárgyalunk.
4. Stabilitás a lineáris közelítés alapján. Linearizáljuk a kétszer folytonosan differenciálható (1') rendszert x=0 megoldás környezetében
![]() Itt
Itt ![]() , X az f nemlineáris része (
, X az f nemlineáris része ( ![]() ).
).
1. Tétel. (Ljapunov aszimptotikus stabilitás, instabilitás a lineáris közelítés alapján). Tekintsük az
![]() rendszert, ahol
rendszert, ahol ![]() ,
, ![]() . Legyenek
. Legyenek ![]() az A mátrix sajátértékei. Ha
az A mátrix sajátértékei. Ha
![]() , akkor az (1'')
rendszer x=0 megoldása Ljapunov értelemben
aszimptotikusan stabilis,
, akkor az (1'')
rendszer x=0 megoldása Ljapunov értelemben
aszimptotikusan stabilis,
![]() , akkor az (1'')
rendszer x=0 megoldása Ljapunov értelemben instabilis.
, akkor az (1'')
rendszer x=0 megoldása Ljapunov értelemben instabilis.
Látható, hogy
a fenti feltételek mellett a nemlineáris rendszer és a linearizált rendszer
lokális viselkedése az origó egy környezetében (a környezet nagysága becsülhető
pl. a korábbiakban említett Ljapunov függvények segítségével) megegyezik. A
stabilitás vizsgálata visszavezethető az A mátrix sajátértékei valós részének
vizsgálatához. A sajátértékek a ![]() karakterisztikus
egyenlet gyökei. A gyökök valós része negativitásának meghatározásához nem
szükséges a gyökök tényleges meghatározása. Igaz ugyanis a
karakterisztikus
egyenlet gyökei. A gyökök valós része negativitásának meghatározásához nem
szükséges a gyökök tényleges meghatározása. Igaz ugyanis a
Routh-Hurwitz kritérium. Tekintsük az ![]() egyenletet. Ezen
egyenlet minden gyöke valós részének negativitásához szükséges és elégséges,
hogy az alábbi H un. Hurwitz mátrix
főminorjainak determinánsai pozitívak legyenek, azaz
egyenletet. Ezen
egyenlet minden gyöke valós részének negativitásához szükséges és elégséges,
hogy az alábbi H un. Hurwitz mátrix
főminorjainak determinánsai pozitívak legyenek, azaz
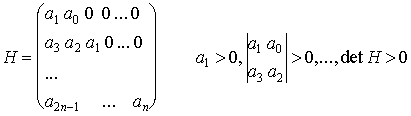 .
. ![]() .
.
A fenti kritériumnál egyszerűbb, de csak szükséges feltétel az aszimptotikus stabilitásra az, ha a karakterisztikus egyenlet minden együtthatójának azonos az előjele.
6. hét: Skalár-,
vektorterek differenciálása.
Vektor-vektor függvények differenciálhatósága. Derivált tenzor és
invariánsai (divergencia, rotáció). Másodrendű differenciáloperátorok (Laplace
operátor).
1. Bevezetés. Az 5-9. hetek anyagában részletesebben tárgyaljuk a T2 (Többváltozós analízis és differenciálegyenletek alapjai) tárgy keretében már bevezetésre került skalár-, illetve vektorterek differenciálásával és integrálásával kapcsolatos kérdéseket. Vizsgálatainkat az alkalmazásokban legtöbbször felmerülő háromdimenziós téren definiált skalár-vektor és vektor-vektor függvényekkel folytatjuk. Bevezetünk egy új jelölésrendszert a "nabla" operátort, mely segítségével egységesen tárgyalható több a korábbiakban már értelmezett fogalom, mint pl. a gradiens, divergencia, rotáció, Laplace operátor.
1. definíció. (Nabla operátor) Nabla operátornak nevezzük és -val jelöljük a
Descartes-féle koordinátarendszerben 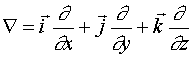 Összefüggésekkel
definiált differenciáloperátort.
Összefüggésekkel
definiált differenciáloperátort.
Megjegyezzük, hogy a vektorokat felül illetve alul húzással jelöljük (a két jelölést egyenértékűnek tekintve). Már itt utalunk arra, hogy a nabla tulajdonságai emlékeztetnek mind a vektorok, mind a deriválás tulajdonságaira.
2. Alapfogalmak. Itt röviden
összefoglaljuk a skalárterek, vektorterek deriválására vonatkozó ismereteinket.
A vizsgálat tárgyai a háromdimenziós tér
D
nyílt, összefüggő tartományán
értelmezett ![]() skalár-vektor,
skalár-vektor, ![]() vektor-vektor
függvények.
vektor-vektor
függvények.
2. Definíció. Az ![]() függvény differenciálható az
függvény differenciálható az ![]() pontban, ha
pontban, ha ![]() ,
, ![]() . Az így kapott d
derivált vektort többféleképpen jelöljük:
. Az így kapott d
derivált vektort többféleképpen jelöljük: 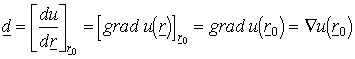 . A nabla operátort
tartalmazó jelölés helyességét magyarázzák az alábbiak
. A nabla operátort
tartalmazó jelölés helyességét magyarázzák az alábbiak 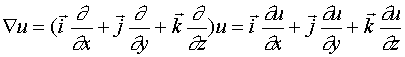 .
.
Tegyük fel,
hogy ![]() deriválhatóak a D -ben,
akkor
deriválhatóak a D -ben,
akkor
![]() ,
, ![]() ,
, 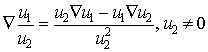 ,
, 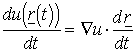 (itt r egy reguláris térgörbe:
(itt r egy reguláris térgörbe: ![]() ).
).
3. Definíció. ![]() függvény differenciálható az
függvény differenciálható az ![]() pontban, ha
pontban, ha ![]() . Az
. Az ![]() a derivált tenzor.
a derivált tenzor.
Felsorolunk néhány a
vektor-vektor függvények deriválására vonatkozó összefüggést (feltesszük, hogy
a bennük szereplő függvények deriválhatóak a D-ben). ![]() ,
, ![]() ( a
( a ![]() a diadikus szorzat,
Descartes koordinátákban a
a diadikus szorzat,
Descartes koordinátákban a ![]() mátrix),
mátrix), 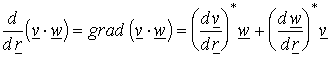 . A * az adjungált operátort (Descartes koordinátákban a
transzponált mátrixot) jelöli.
. A * az adjungált operátort (Descartes koordinátákban a
transzponált mátrixot) jelöli.
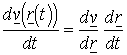 . ( r egy reguláris térgörbe:
. ( r egy reguláris térgörbe: ![]() ).
).
A derivált tenzor, a T2 tárgy keretében már értelmezett, skalár illetve vektor invariánsa (divergencia, rotáció) felírható a nabla operátor segítségével.
Legyen a ![]() függvény differenciálható, D nyílt, összefüggő,
függvény differenciálható, D nyílt, összefüggő, ![]()
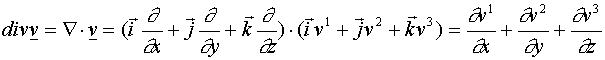 ,
,
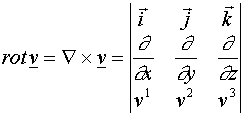 . Az összefüggést
célszerű ebben az alakban megjegyezni, a szimbolikus determináns kifejtésével
adódik a rotáció koordinátás alakja
. Az összefüggést
célszerű ebben az alakban megjegyezni, a szimbolikus determináns kifejtésével
adódik a rotáció koordinátás alakja 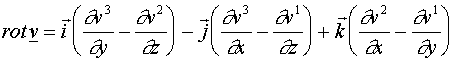 .
.
Befejezésül felírunk néhány invariánsokat tartalmazó összefüggést a nabla operátor segítségével (feltesszük a függvények szükséges számú - egy-, illetve kétszeres - deriválhatóságát):
![]() , azaz
, azaz ![]() .
.
![]() . (Az elsőből jól látszik a deriválás jellege - szorzat
deriváltja, míg a második a vektor jellegre utal - két azonos vektort
tartalmazó vegyes szorzat értéke 0.
. (Az elsőből jól látszik a deriválás jellege - szorzat
deriváltja, míg a második a vektor jellegre utal - két azonos vektort
tartalmazó vegyes szorzat értéke 0.
A Laplace
operátor 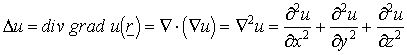 . Megjegyezzük, hogy
amennyiben nem Descartes koordinátákat használunk, akkor a Laplace operátor
kifejezése módosul: gömbi koordinátákban
. Megjegyezzük, hogy
amennyiben nem Descartes koordinátákat használunk, akkor a Laplace operátor
kifejezése módosul: gömbi koordinátákban 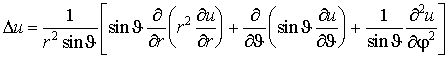 , henger
koordináták-ban
, henger
koordináták-ban 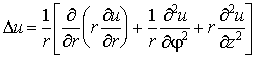 .
.
7-8. hét: Vektorterek
integrálása, integrálátalakító tételek.
Vektor-vektor függvények vonalmenti
integrálja. A vonalintegrál szemléletes jelentése, munka, cirkuláció.
Vektor-vektor függvények felületmenti integrálja. Fluxus.
Integrálátalakító tételek (
Gauss-Osztrogradszkij, Stokes, Green tételek három illetve két dimenzióban, és
alkalmazásaik (megmaradási elvek).
1. Bevezetés. A 7. illetve 8. hetek anyagának összevonását az indokolja, hogy az itt tárgyalandó két legfontosabb integrálfogalom (vonalintegrál, felületi integrál) már a T2 tárgy keretében bevezetésre került, viszont mind tartalmuk megvilágításában, mind kiszámításuk módszereiben döntő szerepet játszanak az integrálátalakító tételek. Többek között ezen tételek lehetőséget adnak a divergencia illetve rotáció fogalmának mélyebb megértésére is.
2. Integrálfogalmak. A továbbiakban a ![]() folytonos
vektor-vektor függvényt vizsgáljuk a D nyílt, összefüggő tartományon (egyes esetekben további simasági,
illetve a tartományra vonatkozó feltételek is szükségesek, akkor ezt külön
jelezzük).
folytonos
vektor-vektor függvényt vizsgáljuk a D nyílt, összefüggő tartományon (egyes esetekben további simasági,
illetve a tartományra vonatkozó feltételek is szükségesek, akkor ezt külön
jelezzük).
Legyen egy reguláris térgörbe a D-ben, azaz
![]() .
.
Megjegyezzük, hogy a reguláris térgörbe egy leképezés, de külön említés nélkül -val jelöljük (és reguláris térgörbének nevezzük) a leképezés képhalmazát is a háromdimenziós térben.
A vektormező görbe mentén vett vonalmenti integrálja alatt a következő valós számot értjük
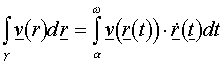 .
.
A vonalmenti
integrál szemléletes jelentése pl. a munka. Ha a görbe zárt, akkor szokás cirkulációról beszélni. A görbementi
integrál csak a görbétől, mint ponthalmaztól és annak irányításától (![]() érintővektor irányától) függ.
érintővektor irányától) függ.
Legyen F egy reguláris felület a D-ben, azaz
![]() .
.
T nyílt és összefüggő halmaz a síkon. Megjegyezzük, hogy az F reguláris felület egy leképezés, de külön említés nélkül F-el jelöljük (és reguláris felületnek nevezzük) a leképezés képhalmazát is a háromdimenziós térben.
A vektormező F felület mentén vett felületi integrálja alatt a következő valós számot értjük
![]() .
.
A felületi
integrál szemléletes jelentése pl. a felületen időegység alatt átáramló anyag
mennyisége. Ha a felület zárt, akkor szokás fluxusról
beszélni. A felületi integrál csak a felülettől, mint ponthalmaztól és annak
irányításától (![]() normálvektor irányától) függ.
normálvektor irányától) függ.
3. Gauss-Osztrogradszkij tétel. Az integrálátalakító tételek matematikai gyökere a Newton-Leibniz formula, melyet kimondhatunk úgy is, hogy egy függvény deriváltjának integrálja a tartományon megegyezik a függvény integráljával a tartomány határán (egydimenziós esetben a tartomány egy szakasz, határa két pont, az ezek mentén vett integrál a két helyettesítési érték különbsége). Bonyolultabb integráloknál a "deriválás" fogalmát módosítani kell, de az eredmény igaz marad. Az egész elmélet kifejtésére itt nincs módunk, ellenben megfogalmazunk néhány az alkalmazások szempontjából fontos speciális esetet. A Gauss-Osztrogradszkij tétel tekinthető mindennemű megmaradási tétel (anyag, energia stb.) matematikai kifejezésének.
1. Tétel. (Gauss-Osztrogradszkij)
Legyen F egyszerű zárt reguláris
felület (a teret F három diszjunkt részre osztja - ![]() , melyek közül a V korlátos) "kifelé mutató"
normálvektorral (a normálvektor talppontjához közeli pontok a W-be esnek), legyen
, melyek közül a V korlátos) "kifelé mutató"
normálvektorral (a normálvektor talppontjához közeli pontok a W-be esnek), legyen ![]() folytonosan
differenciálható,
folytonosan
differenciálható, ![]() , akkor
, akkor ![]() .
.
1. Példa.
Számítsuk ki az origó középpontú, egységsugarú F gömbfelületen időegység alatt kiáramló
folyadékmennyiséget, ha a folyadék sebessége
![]() .
.
Megoldás.
A feladat az ![]() integrál kiszámítása.
Ez történhet
integrál kiszámítása.
Ez történhet
a felületi integrál szemléletes jelentéséből, mivel az
egységgömb felületén a ![]() normális irányú
egységvektort ad, így a keresett integrál értéke az egységgömb felszíne, azaz
normális irányú
egységvektort ad, így a keresett integrál értéke az egységgömb felszíne, azaz ![]() .
.
a felületi integrál definíciójából, a gömbfelület
parametrizálásával, ahogy ezt megtettük a T2 kurzusban (10. ... Vektormező
felületi integrálja, alkalmazások.). Ott félgömbre számítva ![]() adódott, ahonnan a
szimmetria miatt egész gömbre
adódott, ahonnan a
szimmetria miatt egész gömbre ![]() .
.
az imént megfogalmazott Gauss-Osztrogradszkij tétel
segítségével. A tétel feltételei nyilvánvalóan teljesülnek, így ![]() , vagyis elegendő a jobb oldali integrált kiszámolni. Mivel
, vagyis elegendő a jobb oldali integrált kiszámolni. Mivel
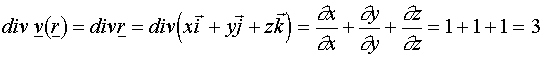 ,
,
a jobb
oldali integrál ![]() , vagyis az egységgömb térfogatának háromszorosa
, vagyis az egységgömb térfogatának háromszorosa ![]() .
.
A Gauss-Osztrogradszkij tétel lehetővé teszi a divergencia szemléletes jelentése (lokális forráserősség sűrűség) precizírozását.
2. Tétel. Legyen ![]() folytonosan
differenciálható,
folytonosan
differenciálható, ![]() ,
, ![]() egyszerű zárt
reguláris egymásba ágyazott felületek sorozata, amely az
egyszerű zárt
reguláris egymásba ágyazott felületek sorozata, amely az ![]() pontra zsugorodik
(azaz az
pontra zsugorodik
(azaz az ![]() -ek által határolt
-ek által határolt ![]() térrészek mérhető
térfogatúak,
térrészek mérhető
térfogatúak, ![]() eleme minden
eleme minden ![]() -nek,
-nek, ![]() átmérője nullához
tart -így természetesen
átmérője nullához
tart -így természetesen ![]() ), akkor a vektor-vektor függvény
), akkor a vektor-vektor függvény ![]() -nekre vonatkozó átlagos forráserősségeinek sorozata
konvergens és a divergenciához tart
-nekre vonatkozó átlagos forráserősségeinek sorozata
konvergens és a divergenciához tart
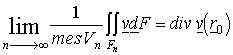 .
.
Bizonyítás.
(vázlat) Az ![]() által határolt
térrészekre felírva a Gauss-Osztrogradszkij tételt, és a hármas integrálra
alkalmazva az integrálközéptételt
adódik az
által határolt
térrészekre felírva a Gauss-Osztrogradszkij tételt, és a hármas integrálra
alkalmazva az integrálközéptételt
adódik az ![]() egyenlőség (
egyenlőség (![]() ). Innen a térfogattal átosztva és figyelembe véve, hogy az
). Innen a térfogattal átosztva és figyelembe véve, hogy az ![]() -ek által határolt
-ek által határolt ![]() térrészek az
térrészek az ![]() pontra
"zsugorodnak", már megkapjuk az eredményt.
pontra
"zsugorodnak", már megkapjuk az eredményt.
4. Stokes tétel. A Gauss-Osztrogradszkij tételben egy háromdimenziós térrészen illetve az őt határoló kétdimenziós zárt felületen integráltunk, a deriválás a nabla operátort jelentette. A most megfogalmazandó Stokes tételben a tartomány a háromdimenziós tér egy kétdimenziós felülete, határa pedig egy zárt görbe lesz.
3. Tétel. (Stokes) Legyen ![]() reguláris felületdarab,
reguláris felületdarab, ![]() irányított egyszerű reguláris zárt felületi görbe az
irányított egyszerű reguláris zárt felületi görbe az ![]() -en.
-en. ![]() normálvektorát irányítsuk úgy, hogy annak irányából nézve a
normálvektorát irányítsuk úgy, hogy annak irányából nézve a ![]() -n kijelölt haladási irány pozitív (az óra járásával
ellentétes). Jelöljük F-el az
-n kijelölt haladási irány pozitív (az óra járásával
ellentétes). Jelöljük F-el az ![]() -nek a
-nek a ![]() görbe által határolt
darabját. Legyen
görbe által határolt
darabját. Legyen ![]() folytonosan
differenciálható,
folytonosan
differenciálható, ![]() . Akkor
. Akkor ![]() .
.
A Stokes tétel lehetővé teszi a rotáció szemléletes jelentése (lokális örvényesség) precizírozását.
4. Tétel. Legyen ![]() , jelöljük
, jelöljük ![]() -el a felület e pontbeli normálvektorát. Tekintsük a
-el a felület e pontbeli normálvektorát. Tekintsük a ![]()
![]() egyszerű zárt
reguláris egymásba ágyazott felületi görbék sorozatát, amely az
egyszerű zárt
reguláris egymásba ágyazott felületi görbék sorozatát, amely az ![]() pontra zsugorodik
(azaz az
pontra zsugorodik
(azaz az ![]() -ek által határolt
-ek által határolt ![]() felületdaraboknak az
felületdaraboknak az ![]() eleme,
eleme, ![]() átmérője nullához
tart -így természetesen a felszínük is nullához tart). Legyen
átmérője nullához
tart -így természetesen a felszínük is nullához tart). Legyen ![]() folytonosan
differenciálható. Akkor
folytonosan
differenciálható. Akkor 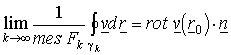 .
.
A tétel
bizonyításától eltekintünk. A bal oldali határértékben szereplő kifejezés
"durván" az ![]() irányra merőleges
síkban levő kis zárt görbe egyszeri körüljárása során végzett átlagos munkát
(lokális örvényesség) jelenti, amit ilyenformán a rotáció adott irányú
komponense mér. Megjegyezzük, hogy "jó" erőterekre (a
potenciálosokra, mint pl. a gravitációs erőtér) ezen integrálok, munkák
zérussal egyenlők, így a rotáció is azonosan nulla lesz. Ennek a kérdéskörnek
szenteljük a következő, 9. hét anyagát.
irányra merőleges
síkban levő kis zárt görbe egyszeri körüljárása során végzett átlagos munkát
(lokális örvényesség) jelenti, amit ilyenformán a rotáció adott irányú
komponense mér. Megjegyezzük, hogy "jó" erőterekre (a
potenciálosokra, mint pl. a gravitációs erőtér) ezen integrálok, munkák
zérussal egyenlők, így a rotáció is azonosan nulla lesz. Ennek a kérdéskörnek
szenteljük a következő, 9. hét anyagát.
Végezetül
leírjuk a nabla szimbolika alkalmazásával az két integrál átalakító tételünket
egy szimmetrikusabb alakban (a térrész illetve felület határára a ![]() jelölést
használva
jelölést
használva ![]() :
:
Gauss-Osztrogradszkij
tétel - ![]() -
- ![]() ,
,
Stokes tétel - ![]() -
- ![]() .
.
Ezekben a jelölésekben már jobban szembeötlő a két tétel közös matematikai eredete.
5. Szimmetrikus Green-formula. A most
közlendő tétel egyrészt tekinthető a parciális integrálás általánosításának,
másrészt utal arra, hogy a Laplace operátor (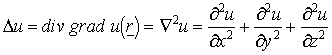 ) tulajdonságai sokban hasonlítanak a szimmetrikus véges
dimenziós lineáris operátorokhoz.
) tulajdonságai sokban hasonlítanak a szimmetrikus véges
dimenziós lineáris operátorokhoz.
5. Tétel. (Green) Legyen F egyszerű zárt reguláris felület, kifelé
mutató normálvektorral, V az F által határolt korlátos térrész.
Legyenek ![]() kétszer folytonosan
differenciálható skalár-vektor függvények,
kétszer folytonosan
differenciálható skalár-vektor függvények, ![]() . Ekkor
. Ekkor
![]() .
.
Bizonyítás.
(vázlat) Tekintsük az ![]() felületi integrált. A
Gauss-Osztrogradszkij tétel értelmében illetve alkalmazva a megfelelő
deriválási szabályokat
felületi integrált. A
Gauss-Osztrogradszkij tétel értelmében illetve alkalmazva a megfelelő
deriválási szabályokat ![]() . Megcserélve a két
változót
. Megcserélve a két
változót ![]() . Kivonva a két
kifejezést egymásból adódik az állítás.
. Kivonva a két
kifejezést egymásból adódik az állítás.
Amennyiben
átírjuk a nabla operátor segítségével a bizonyításban szereplő ![]() integrált, akkor az alábbi kifejezést kapjuk
integrált, akkor az alábbi kifejezést kapjuk ![]() , ami átrendezve a parciális integrálásnak megfelelő
, ami átrendezve a parciális integrálásnak megfelelő ![]() alakot ölti.
alakot ölti.
A 11. hét
anyagában (Fourier sorok) részletesebben tárgyalásra kerül a skalárszorzat
általánosítása függvényterek esetére. Itt csak azt írjuk fel, hogy a V téren megadott f,g két háromváltozós függvény skaláris szorzata alatt a ![]() integrál értékét
értjük. Ha a
integrál értékét
értjük. Ha a ![]() Green formulában a
bal oldali integrál 0 (ami igaz pl. ha vagy a függvények, vagy gradiensük 0 a
határoló felületen), akkor a
Green formulában a
bal oldali integrál 0 (ami igaz pl. ha vagy a függvények, vagy gradiensük 0 a
határoló felületen), akkor a ![]() kifejezésből
átrendezéssel
kifejezésből
átrendezéssel ![]() , ami megfelel az
, ami megfelel az ![]() skalárszorzatok
egyenlőségének. Ez pedig az
skalárszorzatok
egyenlőségének. Ez pedig az ![]() lineáris szimmetrikus
operátorok (mátrixok) jól ismert tulajdonsága
lineáris szimmetrikus
operátorok (mátrixok) jól ismert tulajdonsága ![]() .
.
6. Kétdimenziós integrálátalakító tételek.
Az előbbi a Newton-Leibniz formula néhány háromdimenziós vektor-vektor
függvényekre vonatkozó általánosítását közöltük (Különösen a rotációt tartalmazó
Stokes tétel jellegzetesen három dimenziós). Most röviden kitérünk a ![]() kétdimenziós
vektormezők esetére. Számításainkat Descartes-féle koordinátákban végezzük ,
így
kétdimenziós
vektormezők esetére. Számításainkat Descartes-féle koordinátákban végezzük ,
így ![]() ,
, ![]() . Tekintsünk a sík D tartományában
egy reguláris egyszerű zárt
görbét, jelöljük T-vel az általa
határolt mérhető korlátos síkhalmazt (
. Tekintsünk a sík D tartományában
egy reguláris egyszerű zárt
görbét, jelöljük T-vel az általa
határolt mérhető korlátos síkhalmazt (![]() ). A T tartományt parametrizáljuk
"természetes" módon, azaz
). A T tartományt parametrizáljuk
"természetes" módon, azaz ![]() . Ezen körülmények között a rotáció, illetve a felületelem
vektor
. Ezen körülmények között a rotáció, illetve a felületelem
vektor 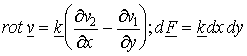 -nek adódnak.
-nek adódnak.
6. Tétel. (síkbeli Stokes) Legyen ![]() folytonosan
differenciálható, reguláris egyszerű zárt
görbe, T a belseje,
folytonosan
differenciálható, reguláris egyszerű zárt
görbe, T a belseje, ![]() , akkor
, akkor
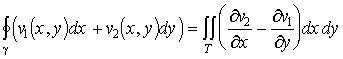 .
.
Bizonyítás.
Alkalmazzuk az ![]() Stokes tételt. A
baloldali vonalintegrál koordinátás alakban éppen
Stokes tételt. A
baloldali vonalintegrál koordinátás alakban éppen ![]() . Felhasználva felületi integrál definícióját és a
. Felhasználva felületi integrál definícióját és a 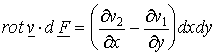 egyenlőséget, a jobb oldali integrálra a
egyenlőséget, a jobb oldali integrálra a 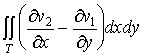 kettősintegrált
kapjuk.
kettősintegrált
kapjuk.
Tekintsük a ![]() vektormezőt.
Divergenciája nyilvánvalóan
vektormezőt.
Divergenciája nyilvánvalóan 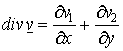 . Vezessük be a
. Vezessük be a ![]() vektormezőt és
alkalmazzuk rá az előbbi síkbeli Stokes
tételt. A kapott eredmény
vektormezőt és
alkalmazzuk rá az előbbi síkbeli Stokes
tételt. A kapott eredmény 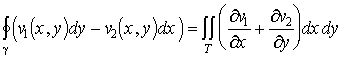 . A mennyiben bevezetjük a
. A mennyiben bevezetjük a ![]() ívelem normálvektort,
akkor a bal oldali vonalintegrál felírható
ívelem normálvektort,
akkor a bal oldali vonalintegrál felírható ![]() alakban. Az eddigiek
összefoglalásaként megfogalmazható
alakban. Az eddigiek
összefoglalásaként megfogalmazható
7. Tétel. (síkbeli Gauss-Osztrogradszkij)
Legyen ![]() folytonosan
differenciálható, reguláris egyszerű zárt
görbe, T a belseje,
folytonosan
differenciálható, reguláris egyszerű zárt
görbe, T a belseje, ![]() , akkor
, akkor
![]() .
.
9. hét: Potenciálelmélet.
A potenciálelmélet elemei. Potenciálos, konzervatív, örvénymentes
vektormezők. Egyszeresen összefüggő tartomány. Harmonikus függvények. Utalás
görbevonalu koordinátarendszerekre.
1. Bevezetés. Az elmúlt hetek anyagában a Newton-Leibniz formula
általánosításával foglalkoztunk vektorterek esetére. Ismert, hogy a vektoterek
görbementi integrálja általában nem csak a görbe két végpontjától, hanem az
úttól is függ, amely mentén integrálunk. A kérdés matematikai magyarázata az,
hogy amennyiben a dimenzió nagyobb, mint egy, akkor egy függvénynek nem okvetlenül
létezik primitívfüggvénye. Azon ![]() vektormezőkre,
melyeknek van primitív függvényük (
vektormezőkre,
melyeknek van primitív függvényük (![]() ), lényegében érvényben marad a Newton-Leibniz formula. A
probléma fizika háttere az örvényesség jelenségében keresendő.
), lényegében érvényben marad a Newton-Leibniz formula. A
probléma fizika háttere az örvényesség jelenségében keresendő.
2. Fogalmak. A továbbiakban vizsgálatunk
tárgya a ![]() folytonosan
differenciálható vektor-vektor függvény a
D
nyílt, összefüggő tartományon.
folytonosan
differenciálható vektor-vektor függvény a
D
nyílt, összefüggő tartományon.
1. Definíció. (potenciálosság) Azt
mondjuk, hogy a ![]() vektormező potenciálos a D tartományban, ha létezik olyan
vektormező potenciálos a D tartományban, ha létezik olyan ![]() differenciálható skalár-vektor függvény, melyre
differenciálható skalár-vektor függvény, melyre ![]() . Az u függvényt potenciálfüggvénynek
nevezzük.
. Az u függvényt potenciálfüggvénynek
nevezzük.
2. Definíció. (konzervativitás) Azt
mondjuk, hogy a ![]() vektormező konzervatív a D tartományban, ha bármely
vektormező konzervatív a D tartományban, ha bármely ![]() reguláris zárt görbén
vett vonalmenti integrál értéke nulla, azaz
reguláris zárt görbén
vett vonalmenti integrál értéke nulla, azaz
![]() .
.
Megjegyezzük, hogy ezen definíció ekvivalens azzal, hogy két pontot összekötő bármely két görbe mentén megegyezik a vonalmenti integrál értéke.
3. Definíció. (örvénymentesség) Azt
mondjuk, hogy a ![]() vektormező örvénymentes (rotációmentes) a D tartományban, ha a vektormező
rotációja azonosan nulla a D-ben,
azaz
vektormező örvénymentes (rotációmentes) a D tartományban, ha a vektormező
rotációja azonosan nulla a D-ben,
azaz ![]() .
.
A potenciálelmélet alaptétele kimondásához a fent már vázolt fogalmak és feltételek mellett egy további feltétel szükséges a D tartomány egyszeresen összefüggősége. Ezt egy több lépéses definicíó sorozattal adjuk meg.
3. Definíció. (egyszeres összefüggőség)
egy síktartományt egyszeresen összefüggőnek nevezünk, ha minden benne haladó zárt görbével együtt annak belsejét is tartalmazza.
egy F felületdarabot egyszeresen összefüggőnek nevezünk, ha egy egyszeresen összefüggő síktartomány képe.
egy ![]() tartományt
egyszeresen összefüggőnek nevezünk, ha bármely
tartományt
egyszeresen összefüggőnek nevezünk, ha bármely ![]() egyszerű reguláris
zárt görbére illeszthető F egyszeresen
összefüggőnek reguláris felületdarab a D-ben, mely határoló görbéje .
egyszerű reguláris
zárt görbére illeszthető F egyszeresen
összefüggőnek reguláris felületdarab a D-ben, mely határoló görbéje .
3. A potenciálelmélet alaptétele. Legyen
![]() folytonosan
differenciál-ható vektor-vektor függvény a
D
nyílt, egyszeresen összefüggő tartományon. Akkor az alábbi három
állítás ekvivalens
folytonosan
differenciál-ható vektor-vektor függvény a
D
nyílt, egyszeresen összefüggő tartományon. Akkor az alábbi három
állítás ekvivalens
(i) a
![]() vektormező potenciálos,
vektormező potenciálos,
(ii) a ![]() vektormező konzervatív,
vektormező konzervatív,
(iii) a ![]() vektormező örvénymentes.
vektormező örvénymentes.
A tételt itt most nem bizonyítjuk. Bizonyításánál felhasználásra kerülnek Newton-Leibniz formula igazolásához hasonló gondolatok (integrálfüggvény), a nabla operátor tulajdonságai, a Stokes tétel.
A
potenciálelmélet alaptétele lehetővé teszi potenciálos vektormezők görbementi
integráljának gyorsabb kiszámítását. Tegyük fel, hogy meg kell határoznunk a 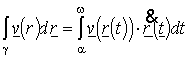 görbementi integrál
értékét (pl. munkát). A módszer a következő
görbementi integrál
értékét (pl. munkát). A módszer a következő
1. Ellenőrizzük,
hogy létezik-e olyan egyszeresen összefüggő
D' részhalmaza a vektormező értelmezési tartományának, melyre ![]() ,
,
2. Ellenőrizzük,
hogy örvénymentes-e a vektormező,azaz ![]() . Emlékeztetünk arra, hogy ez a
. Emlékeztetünk arra, hogy ez a 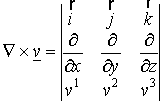 szimbolikus
determináns kiszámításával történhet.
szimbolikus
determináns kiszámításával történhet.
3. Amennyiben az előbbi két feltétel teljesül, akkor érvényben van a potenciálelmélet alaptétele. Meghatározunk egy u potenciálfüggvényt (a potenciálfüggvények egymástól csak konstansban térnek el). A potenciálfüggvény megkeresésére több módszer létezik
elemi integrálással megoldjuk a 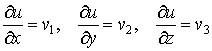 parciális
differenciálegyenlet-rendszert,
parciális
differenciálegyenlet-rendszert,
egy rögzített pontból kiszámítjuk a vonalintegrál értékét a tartomány egy tetszőleges pontjába egy speciálisan választott (pl. a tengelyekkel párhuzamos) út mentén.
4. A
potenciálfüggvény segítségével felírható a vonalintegrál értéke, mint a
potenciálfüggvény a görbe két végpontjában tekintett helyettesítési értéke
különbsége 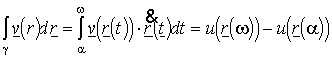 .
.
4. Divergencia és rotációmentes vektormezők.
A ![]() a D nyílt, összefüggő tartományon
folytonosan differenciálható vektor-vektor függvényt divergenciamentesnek nevezzük, ha
a D nyílt, összefüggő tartományon
folytonosan differenciálható vektor-vektor függvényt divergenciamentesnek nevezzük, ha 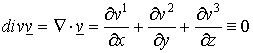 . A Gauss-Osztrograszkij tételből látszik, hogy minden F egyszerű zárt reguláris felületre,
. A Gauss-Osztrograszkij tételből látszik, hogy minden F egyszerű zárt reguláris felületre, ![]()
![]() , vagyis a zárt felületek mentén vett integrálok nullák. Ez
egyébként ekvivalens avval, hogy tetszőleges
D-beli felületekre, melyeket
ugyanaz a görbe határol a felületi
integrálok értékei megegyeznek.
, vagyis a zárt felületek mentén vett integrálok nullák. Ez
egyébként ekvivalens avval, hogy tetszőleges
D-beli felületekre, melyeket
ugyanaz a görbe határol a felületi
integrálok értékei megegyeznek.
Az
alkalmazásokban különösen fontos szerepet játszanak az egyszerre divergencia és
rotációmentes vektormezők (![]() ,
, ![]() ). A potenciálelméletből adódóan ilyenkor létezik u:
). A potenciálelméletből adódóan ilyenkor létezik u: ![]() . Innen a
. Innen a ![]() egyenlőségből adódóan
egyenlőségből adódóan
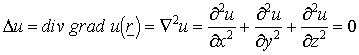 . Emlékeztetünk arra, hogy a Laplace operátorra 0 értéket adó függvényeket harmonikus
függvényeknek nevezzük. (Megjegyezzük, hogy pl. a gravitációs erőtér
potenciálfüggvénye harmonikus.)
. Emlékeztetünk arra, hogy a Laplace operátorra 0 értéket adó függvényeket harmonikus
függvényeknek nevezzük. (Megjegyezzük, hogy pl. a gravitációs erőtér
potenciálfüggvénye harmonikus.)
10. hét: Függvénysorozatok,
sorok
Függvénysorozatok, sorok pontonkénti, egyenletes, abszolút
konvergenciája. Függvénysorozatok,
sorok integrálása, differenciálása, a határfüggvény tulajdonságai.
1. Bevezetés. A matematika alkalmazásai során a különböző modellezendő jelenségeket gyakran függvényekkel írjuk le. Ezen függvények általában bonyolultak, ezért további kezelésük (pl. algebrai, differenciál-, integrálegyenletek megoldása) nagy problémát jelent. Az ilyen feladatok megoldásának szokásos matematikai módszere az, hogy az érintett függvényeket egyszerűbbekkel (pl. polinomok, trigonometrikus polinomok) közelítjük. Ez az okoskodás is bizonyítja a függvénysorozatok, sorok elmélete fontosságát. Óravázlatunkban két hetet szentelünk a kérdéskörnek. E hét anyaga az általános elméletet tárgyalja, a 11. héten térünk ki a fentebb már említett két legfontosabb speciális esetek (Taylor sorok, Fourier sorok) vizsgálatára.
2. Alapfogalmak. Tekintsük az ![]() függvényekből álló
sorozatot. Feltesszük, hogy ezen függvények értelmezési tartománya közös és
ugyanabba a halmazba képeznek (jelen esetben az egyszerűség kedvéért mindkettő
a valós számok részhalmaza), azaz
függvényekből álló
sorozatot. Feltesszük, hogy ezen függvények értelmezési tartománya közös és
ugyanabba a halmazba képeznek (jelen esetben az egyszerűség kedvéért mindkettő
a valós számok részhalmaza), azaz ![]() .
.
1. Definíció (pontonkénti konvergencia).
Azt mondjuk, hogy az ![]() ,
, ![]() függvénysorozat
pontonként konvergál a
függvénysorozat
pontonként konvergál a ![]() halmazon az
halmazon az ![]() függvényhez
(jelölés
függvényhez
(jelölés ![]() ), ha
), ha
![]() .
.
Az így definiált konvergencia a legtermészetesebb ugyan, de viselkedése a sorozat határértéke, differenciálása, integrálása szempontjából "nem jó", ezért bevezetjük a következő fogalmat
2. Definíció (egyenletes konvergencia).
Azt mondjuk, hogy az ![]() ,
, ![]() függvénysorozat
egyenletesen konvergál a
függvénysorozat
egyenletesen konvergál a ![]() halmazon az
halmazon az ![]() függvényhez
(jelölés
függvényhez
(jelölés ![]() ), ha
), ha
![]() .
.
A nem konvergens sorozatokat divergensnek nevezzük.
1. példa.
Tekintsük az ![]() függvénysorozatot.
függvénysorozatot.
Könnyen
látható, hogy a sorozat pontonként konvergál a
![]() intervallumon az
intervallumon az ![]() függvényhez (a
számegyenes többi pontjára divergens).
függvényhez (a
számegyenes többi pontjára divergens).
Igazolható,
hogy a sorozat egyenletesen konvergál az azonosan 0 függvényhez a ![]() intervallumok
bármelyikén.
intervallumok
bármelyikén.
Vezessük be a Cauchy konvergencia fogalmát függvénysorozatokra (csak az egyenletes eset definícióját írjuk fel).
3. Definíció (egyenletes Cauchy konvergencia). Azt mondjuk, hogy az
![]() ,
, ![]() függvénysorozat
egyenletesen Cauchy konvergens a
függvénysorozat
egyenletesen Cauchy konvergens a ![]() halmazon, ha
halmazon, ha ![]() .
.
3. Alaptételek.
1. Tétel. A függvénysorozatok egyenletes Cauchy konvergenciája és egyenletes konvergenciája ekvivalensek.
2. Tétel. Folytonos függvények egyenletesen konvergens függvénysorozatának a határfüggvénye is folytonos. Azaz, ha
![]() , akkor
, akkor ![]() .
.
1.Megjegyzés: Az 1.
példában tárgyalt ![]() folytonos függvényekből álló függvénysorozatra a konvergencia
nem lehet egyenletes az egész
folytonos függvényekből álló függvénysorozatra a konvergencia
nem lehet egyenletes az egész ![]() intervallumon, mivel
a határfüggvény
intervallumon, mivel
a határfüggvény ![]() nem folytonos az x=1 pontban.
nem folytonos az x=1 pontban.
3. Tétel. (integrálás). Legyen ![]() , ahol
, ahol ![]() integrálható
függvények az
integrálható
függvények az ![]() intervallumon, akkor
a sorozat elemei integráljának határértéke megegyezik a határfüggvény
integráljával,
intervallumon, akkor
a sorozat elemei integráljának határértéke megegyezik a határfüggvény
integráljával, 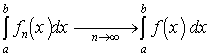 .
.
4. Tétel. (deriválás). Egy D tartományon legyenek az ![]() függvénysorozatra
igazak a következők:
függvénysorozatra
igazak a következők: ![]() ,
, ![]() ,
, ![]() , akkor a határfüggvény deriválható és deriváltja megegyezik
a deriváltfüggvények határértékével,
, akkor a határfüggvény deriválható és deriváltja megegyezik
a deriváltfüggvények határértékével, ![]() .
.
2.Megjegyzés: A numerikus sorozatoknál megismert, a sorozatokkal végzett algebrai műveletekre vonatkozó tételek (elemek összeadása, szorzása stb) érvényben maradnak a függvénysorozatok különböző konvergencia típusaira. Ezeket itt külön nem fogalmazzuk meg.
4. Függvénysorok. Tekintsük az ![]() függvényeket. A
belőlük képezett
függvényeket. A
belőlük képezett 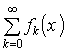 végtelen összeget
függvénysornak nevezzük. A pontos definíciókat az
végtelen összeget
függvénysornak nevezzük. A pontos definíciókat az 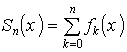 részletösszegek
sorozatával adjuk meg.
részletösszegek
sorozatával adjuk meg.
1(2) Definíció (pontonkénti(egyenletes)
konvergencia). A 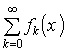 függvénysort
pontonként (egyenletesen) konvergensnek nevezzük, ha a részletösszegek
függvénysort
pontonként (egyenletesen) konvergensnek nevezzük, ha a részletösszegek 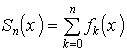 sorozata pontonként
(egyenletesen) konvergens. A határfüggvényt itt összegnek nevezzük és az
sorozata pontonként
(egyenletesen) konvergens. A határfüggvényt itt összegnek nevezzük és az 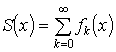 jelölést használjuk.
jelölést használjuk.
3. Definíció (abszolút konvergencia). A 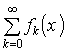 függvénysort abszolút
konvergensnek nevezzük, ha a
függvénysort abszolút
konvergensnek nevezzük, ha a 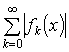 függvénysor
pontonként konvergens.
függvénysor
pontonként konvergens.
3. megjegyzés. A bevezetett háromféle konvergencia között nyilvánvalóan fennáll az, hogy az egyenletes illetve abszolút konvergenciából következik a pontonkénti konvergencia. További implikációk általában nem igazak.
4. megjegyzés. A függvénysorozatokra vonatkozó 1-4. tételek megfelelő terminológiai változtatásokkal (Cauchy konvergencia, az összegfüggvény folytonossága, a függvénysor tagonkénti integrálása, deriválása) érvényben maradnak a függvénysorok esetében is, hasonlóan az algebrai műveletekre vonatkozó tételekhez.
Mivel az egyenletes konvergencia gyakori feltétel az előbbi tételekben végezetül megfogalmazunk egy elégséges feltételt
5. Tétel (Weierstrass kritérium).
Legyenek ![]() függvények olyanok,
hogy
függvények olyanok,
hogy ![]() -re
-re ![]() természetes számra és
a majoráló
természetes számra és
a majoráló ![]() sorozat konvergens.
Akkor a
sorozat konvergens.
Akkor a 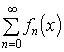 függvénysor abszolút
és egyenletesen konvergens.
függvénysor abszolút
és egyenletesen konvergens.
11. hét: Hatványsorok,
Fourier sorok
Hatványsorok, konvergencia sugár. Fourier
sorok. Fourier sorfejtés, utalás a különböző konvergencia típusokra.
1. Bevezetés. Az előző hét anyagában
részletesen tárgyalásra került a függvénysorok
(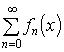 ) általános elmélete. Most az alkalmazásokban legtöbbször
fellépő két speciális esetre: a hatványsorokra (
) általános elmélete. Most az alkalmazásokban legtöbbször
fellépő két speciális esetre: a hatványsorokra ( ![]() ), illetve a Fourier sorokra (
), illetve a Fourier sorokra (![]() ) térünk ki. Az általános elmélet természetesen igaz itt is,
de amikor polinomokkal, trigonometrikus polinomokkal közelítünk, akkor a
konvergencia tartományra, a konvergencia fajtájára (pontonkénti, egyenletes,
abszolút), a sorokkal végzett műveletekre (pl. deriválás, integrálás) további
állítások is igazak.
) térünk ki. Az általános elmélet természetesen igaz itt is,
de amikor polinomokkal, trigonometrikus polinomokkal közelítünk, akkor a
konvergencia tartományra, a konvergencia fajtájára (pontonkénti, egyenletes,
abszolút), a sorokkal végzett műveletekre (pl. deriválás, integrálás) további
állítások is igazak.
2. Hatványsorok. A 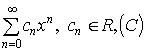 alakú függvénysorokat
hatványsoroknak nevezzük. Aláhúzzuk, hogy mind a c együtthatók, mind az x független változók lehetnek valós, vagy
komplex számok.
alakú függvénysorokat
hatványsoroknak nevezzük. Aláhúzzuk, hogy mind a c együtthatók, mind az x független változók lehetnek valós, vagy
komplex számok.
1.
megjegyzés. Általánosabban hatványsornak a
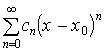 alakú sort nevezzük,
ez azonban a független változó eltolásával átvihető az általunk vizsgált
alakra.
alakú sort nevezzük,
ez azonban a független változó eltolásával átvihető az általunk vizsgált
alakra.
1. Tétel (Cauchy - Hadamard).
Legyen 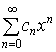 hatványsor,
tekintsük az
hatványsor,
tekintsük az 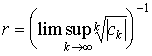 konvergencia sugárnak
nevezett számot. Ekkor
konvergencia sugárnak
nevezett számot. Ekkor 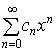 abszolút
konvergens
abszolút
konvergens ![]() esetén,
divergens
esetén,
divergens ![]() -re, az
-re, az ![]() pontokra további
konvergencia vizsgálatok szükségesek. (Ha
pontokra további
konvergencia vizsgálatok szükségesek. (Ha
![]() , akkor csak az
, akkor csak az ![]() -ban konvergens, ha
-ban konvergens, ha ![]() , akkor
, akkor ![]() -re.)
-re.)
2. megjegyzés. A fenti tétel bizonyítása a sorok konvergenciájára vonatkozó gyök kritériumon alapul. Ha a hányados kritériumot alkalmazzuk, akkor az r konvergencia sugárra egy hasonló összefüggés adódik.
3.
megjegyzés. Az előbbi tételben
egyenletes is a konvergencia az r -nél kisebb sugarú intervallumokon
( ![]() -ra, ahol
-ra, ahol ![]() ). Könnyen igazolható, hogy ezen intervallumokon a sor
tagonként differenciálható és integrálható.
). Könnyen igazolható, hogy ezen intervallumokon a sor
tagonként differenciálható és integrálható.
1. példa. Az alábbiakban bemutatunk néhány egyszerű hatványsort (az összegfüggvény, konvergenciasugár megjelölésével)
Mértani sor. 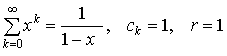 .
.
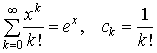 . r számítható a
hányados kritérium alapján, és láthatóan a sor minden x-re konvergens -
. r számítható a
hányados kritérium alapján, és láthatóan a sor minden x-re konvergens - ![]() .
.
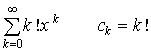 .
. 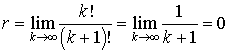 . A sor csak x=0-ra
konvergens, az összege nyilván 0.
. A sor csak x=0-ra
konvergens, az összege nyilván 0.
4.
Megjegyzés. Taylor sorok. Egy az ![]() pont egy
környezetében végtelenszer deriválható függvénynek (
pont egy
környezetében végtelenszer deriválható függvénynek ( ![]() ) felírható a Taylor
sora
) felírható a Taylor
sora 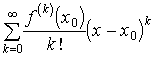 , amely egy hatványsor. (Megjegyezzük, hogy ezen hatványsor
nem okvetlenül konvergens. Ha konvergens, akkor sem okvetlenül az őt generáló
függvényhez tart, amint azt az
, amely egy hatványsor. (Megjegyezzük, hogy ezen hatványsor
nem okvetlenül konvergens. Ha konvergens, akkor sem okvetlenül az őt generáló
függvényhez tart, amint azt az 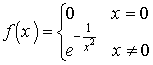 függvény, melynek
Taylor sora
függvény, melynek
Taylor sora 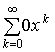 , példája mutatja. A Taylor sor konvergenciája a függvényhez,
amint az az 1. szemeszter matematika anyagában már szerepelt, vizsgálható az
un. Lagrange-féle maradéktag segítségével
, példája mutatja. A Taylor sor konvergenciája a függvényhez,
amint az az 1. szemeszter matematika anyagában már szerepelt, vizsgálható az
un. Lagrange-féle maradéktag segítségével
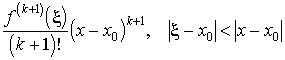 . A konvergenciához
elégséges például
. A konvergenciához
elégséges például ![]() .)
.)
Ezen pont befejezéseként közöljük néhány elemi függvény hatványsorát (az un. Maclaurin sorát)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Fourier sorok. Periodikus függvények
közelítésére használják. Tegyük fel, hogy az
f
függvény integrálható és ![]() szerint periodikus.
Akkor a függvény Fourier sora alatt értjük az
szerint periodikus.
Akkor a függvény Fourier sora alatt értjük az
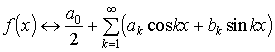
függvénysort, ahol
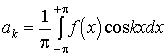 ,
, 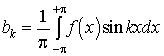 .
.
A ![]() jelölés arra utal,
hogy a sor nem okvetlenül konvergál a függvényhez. A Fourier sorok
konvergenciáját gyakran vizsgálják az általunk bevezetett pontonkénti,
egyenletestől különböző konvergenciák
szempontjából. Mi itt megfogalmazunk egy elégséges (finomítható) állítást, majd
röviden kitérünk más metrikák használatára.
jelölés arra utal,
hogy a sor nem okvetlenül konvergál a függvényhez. A Fourier sorok
konvergenciáját gyakran vizsgálják az általunk bevezetett pontonkénti,
egyenletestől különböző konvergenciák
szempontjából. Mi itt megfogalmazunk egy elégséges (finomítható) állítást, majd
röviden kitérünk más metrikák használatára.
1. Állítás. Az f folytonos és szakaszonként folytonosan differenciálható ![]() szerint periodikus
függvény Fourier sora pontonként konvergál a függvényhez.
szerint periodikus
függvény Fourier sora pontonként konvergál a függvényhez.
Az alábbiakban
vázlatosan ismertetjük a négyzetesen
integrálható függvények elméletének alapjait, ami magyarázatot ad a Fourier
együtthatók alakjára is. Az f valós
![]() szerint periodikus
függvényt négyzetesen integrálhatónak nevezzük (jelölés:
szerint periodikus
függvényt négyzetesen integrálhatónak nevezzük (jelölés: ![]() ), ha létezik az
), ha létezik az 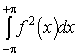 integrál. Ezen
függvényekre értelmezhető a skaláris
szorzat: legyen
integrál. Ezen
függvényekre értelmezhető a skaláris
szorzat: legyen ![]() , a két függvény
skaláris szorzata
, a két függvény
skaláris szorzata 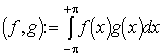 . A skaláris szorzat segítségével - hasonlóan az
. A skaláris szorzat segítségével - hasonlóan az ![]() tér geometriájához -
definiálhatjuk egy függvény hosszát (
tér geometriájához -
definiálhatjuk egy függvény hosszát ( ![]() ), két függvény
merőlegességét (
), két függvény
merőlegességét ( ![]() ). Könnyen
igazolható, hogy az
). Könnyen
igazolható, hogy az ![]() függvények ortonormált függvényrendszert alkotnak
(a hosszúságuk 1 és kölcsönösen merőlegesek egymásra). Innen már adódik, hogy a
Fourier sor nem más, mint az f függvény a trigonometrikus alapfüggvények (
függvények ortonormált függvényrendszert alkotnak
(a hosszúságuk 1 és kölcsönösen merőlegesek egymásra). Innen már adódik, hogy a
Fourier sor nem más, mint az f függvény a trigonometrikus alapfüggvények (![]() ) által generált bázisban tekintett felbontása. Igazolható,
hogy a Fourier sor az
) által generált bázisban tekintett felbontása. Igazolható,
hogy a Fourier sor az ![]() tér metrikájában
(ahol a távolság a függvényértékek különbsége négyzetének integrálja) mindig
konvergál a függvényhez.
tér metrikájában
(ahol a távolság a függvényértékek különbsége négyzetének integrálja) mindig
konvergál a függvényhez.
4.
megjegyzés. Ha a Fourier sor csak véges sok elemet tartalmaz (vagyis 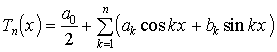 alakú trigonometrikus
polinom), akkor az együtthatók gyakran egyszerűbben számíthatók elemi
azonosságok, illetve a trigonometrikus függvények komplex alakja -
alakú trigonometrikus
polinom), akkor az együtthatók gyakran egyszerűbben számíthatók elemi
azonosságok, illetve a trigonometrikus függvények komplex alakja - ![]() ,
, ![]() - segítségével.
- segítségével.
5.
megjegyzés. Ha a függvényünk f ![]() szerint periodikus.
Akkor a függvény Fourier sora alatt értjük az
szerint periodikus.
Akkor a függvény Fourier sora alatt értjük az
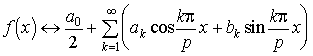
függvénysort, ahol
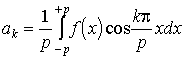 ,
, 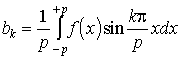 .
.
12. hét: Komplex
függvénytan
Komplex függvénytan alapjai.
Deriválás, analitikus függvény. Konformis leképezések.
1. Bevezetés. A komplex számok, komplex függvénytan felfedezése egyrészről a matematika belső fejlődésének kiemelkedő teljesítménye (gondoljunk pl. az algebrai egyenletrendszerek megoldhatóságára), másrészről már eddig is sok fontos alkalmazással bír (pl. az elektromosságtan, áramlástan terén). Módszereiben kiindulásként a már megismert egyváltozós valós analízis illetve a síkbeli vektormezők elmélete szolgálhat. Kurzusunk 2 hetet szentel e témának, melyben az első hét durván a differenciálszámítást, a második az integrálszámítást érinti.
![]()
![]()
2. Egyváltozós komplex függvények és deriválásuk
Egyváltozós
komplex függvény alatt a komplex számsíkot sajátmagára képező függvényeket ( ![]() ) értjük. A független
változót szokásosan z-vel jelölve, az felírható valós,
képzetes része (x,y) segítségével,
illetőleg az (x,y) értékek visszafelé
kifejezhetőek z-vel és
konjugáltjával. Igazak a következő összefüggések
) értjük. A független
változót szokásosan z-vel jelölve, az felírható valós,
képzetes része (x,y) segítségével,
illetőleg az (x,y) értékek visszafelé
kifejezhetőek z-vel és
konjugáltjával. Igazak a következő összefüggések
 .
.
Hasonlóan a függvényérték is felbontható valós (u) illetve képzetes (v) részre
![]() .
.
1. Példa.
Keressük meg az ![]() függvény valós illetve
képzetes részét (
függvény valós illetve
képzetes részét (![]() ).
).
Megoldás. ![]() , mivel
(emlékeztetünk, hogy
, mivel
(emlékeztetünk, hogy ![]() ).
). ![]() .
.
2. Példa.
Legyenek egy komplex függvény valós, képzetes részei: 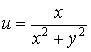 ,
, 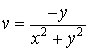 . Írjuk fel a
függvényt z függvényeként.
. Írjuk fel a
függvényt z függvényeként.
Megoldás. 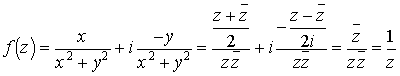 .
.
1. Definíció. Azt mondjuk, hogy az ![]() komplex függvény differenciálható a D nyílt tartományon, ha minden
komplex függvény differenciálható a D nyílt tartományon, ha minden ![]() -re létezik az alábbi
határérték (amit így jelölünk)
-re létezik az alábbi
határérték (amit így jelölünk) ![]() .
.
Az előbbi
definíció felírható ekvivalens alakban az
f
megváltozása segítségével ![]() , ahol
, ahol ![]() .
.
1. Példa
(folytatás) Keressük meg az ![]() függvény deriváltját.
függvény deriváltját.
Megoldás.
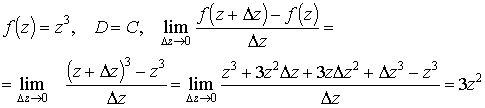
3. példa. Vizsgáljuk
az ![]() függvény
deriválhatóságát.
függvény
deriválhatóságát.
Megoldás.
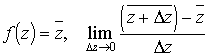 nem létezik, mivel
nem létezik, mivel
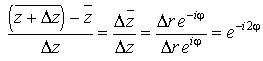 egy -től függő kifejezést ad (Itt
áttértünk a z változóban exponenciális
alakra:
egy -től függő kifejezést ad (Itt
áttértünk a z változóban exponenciális
alakra: ![]() ).
).
Az ![]() függvény
deriválhatósága vizsgálható valós (u)
illetve képzetes (v) része
segítségével.
függvény
deriválhatósága vizsgálható valós (u)
illetve képzetes (v) része
segítségével.
1. Tétel (Cauchy-Riemann feltételek). Az
![]() függvény akkor és
csak akkor differenciálható a D tartományon,
ha valós, képzetes részei totálisan differenciálhatók és kielégítik a
függvény akkor és
csak akkor differenciálható a D tartományon,
ha valós, képzetes részei totálisan differenciálhatók és kielégítik a 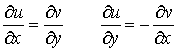 parciális
differenciál--egyenleteket. A függvény deriváltja felírható
parciális
differenciál--egyenleteket. A függvény deriváltja felírható ![]() alakban.
alakban.
Megemlítjük, hogy a Cauchy-Riemann
formulákból könnyen adódik az u , v
függvények harmonikussága, vagyis egy deriválható komplex függvényre
![]() .
.
1. Példa
(2.folytatás) Igazoljuk az ![]() függvény
deriválhatóságát, keressük meg a deriváltját a valós, képzetes rész
segítségével..
függvény
deriválhatóságát, keressük meg a deriváltját a valós, képzetes rész
segítségével..
Megoldás. ![]() . A Cauchy-Riemann feltételeket ellenőrizzük
. A Cauchy-Riemann feltételeket ellenőrizzük 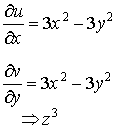 , illetve
, illetve 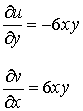 .
.
A derivált
számítható az ![]() kifejezésből
kifejezésből
![]() .
.
3. példa
(folytatás). Vizsgáljuk az ![]() függvény
deriválhatóságát a Cauchy-Riemann feltételek segítségével.
függvény
deriválhatóságát a Cauchy-Riemann feltételek segítségével.
Megoldás.
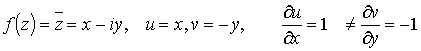 . A feltételék nem teljesülnek, a függvény nem deriválható.
. A feltételék nem teljesülnek, a függvény nem deriválható.
2. Definíció. Ha az ![]() komplex függvény
differenciálható a D nyílt tartományon, akkor analitikus függvénynek nevezzük.
komplex függvény
differenciálható a D nyílt tartományon, akkor analitikus függvénynek nevezzük.
Megjegyzés. A fenti definíció összhangban van a valós analitikus függvény definíciójával. Igaz ugyanis, ha egy komplex függvény differenciálható, akkor végtelen sokszor differenciálható és a Taylor sora a tartomány minden pontjában konvergál a függvényhez.
Mind a fenti megjegyzés, mind a Cauchy-Riemann formula lehetőséget adnak arra, hogy az elemi valós függvényeket kiterjesszük a komplex számsíkra.
4. Példa. Az exponenciális komplex függvény definíciója
hatványsorral: 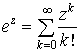 ,
,
valós, képzetes résszel: ![]() .
.
A két
definíció nyilván ekvivalens. Az így kapott exponenciális függvény értelmezett
az egész komplex számsíkon, a valós tengelyen (y=0) a valós exponenciális függvényt adja (a soros definícióra ez
triviális, a másiknál ![]() ). Az exponenciális komplex függvény sok
érdekes tulajdonsággal bír (pl.
). Az exponenciális komplex függvény sok
érdekes tulajdonsággal bír (pl. ![]() periodikus), és
segítségével felírható a legtöbb elemi függvény, amint azt az alábbi
összefoglaló táblázat mutatja
periodikus), és
segítségével felírható a legtöbb elemi függvény, amint azt az alábbi
összefoglaló táblázat mutatja
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Konformis leképezések.
A különböző
függvények deriváltjainak szemléletes jelentést tulajdoníthatunk mind
matematikai, mind a különböző alkalmazások szempontjaiból (pl. az egyváltozós
valós függvény deriváltját szemléltethetjük a függvény grafikon érintőjének
meredekségével, vagy a sebességgel stb.). Most az egyváltozós komplex függvény
deriváltjának jelentését világítjuk meg. Legyen ![]() differenciálható,
rögzítsünk le egy
differenciálható,
rögzítsünk le egy ![]() pontot. A függvény megváltozása közelítőleg
felírható
pontot. A függvény megváltozása közelítőleg
felírható ![]() alakban. Ahonnét látszik, hogy a megváltozás egy
alakban. Ahonnét látszik, hogy a megváltozás egy ![]() -vel való szorzás. Mivel egy komplex számmal való szorzás az
abszolút értékével való szorzást (nyújtást), illetve az argumentumának
hozzáadását (az argumentumával való forgatást) jelenti, így a derivált abszolút
értéke a lokális nyújtást, argumentuma a forgatást jelenti (
-vel való szorzás. Mivel egy komplex számmal való szorzás az
abszolút értékével való szorzást (nyújtást), illetve az argumentumának
hozzáadását (az argumentumával való forgatást) jelenti, így a derivált abszolút
értéke a lokális nyújtást, argumentuma a forgatást jelenti (![]() ,
, ![]() ). Ezen okoskodás pontosítható a konformis leképezések
fogalmának bevezetésével.
). Ezen okoskodás pontosítható a konformis leképezések
fogalmának bevezetésével.
2. Definíció. Egy leképezést az értelmezési tartománya egy pontjában konformisnak nevezzük, ha kicsiben aránytartó (az adott ponthoz tartva a képek és az ősök hosszai arányának határértéke állandó) és szögtartó (az adott pontban egymást metsző görbék érintőinek hajlásszöge megegyezik a görbék képei érintőinek hajlásszögével).
2. Tétel. Legyen az ![]() komplex függvény
differenciálható és a
komplex függvény
differenciálható és a ![]() pontban a deriváltja
nem zérus. Akkor a függvény által létesített leképezés a z-ben
konformis.
pontban a deriváltja
nem zérus. Akkor a függvény által létesített leképezés a z-ben
konformis.
1. Példa
(3.folytatás) Vizsgáljuk, hogy hol ad meg konformis leképezést az ![]() függvény. Mivel a
derivált
függvény. Mivel a
derivált ![]() csak a z=0-ban
nulla, így a leképezés az origó kivételével mindenhol konformis. Az origóban
könnyen láthatóan nem lesz szögtartó, mivel az origón áthaladó görbék által
bezárt szögek a leképezésnél megháromszorozódnak.
csak a z=0-ban
nulla, így a leképezés az origó kivételével mindenhol konformis. Az origóban
könnyen láthatóan nem lesz szögtartó, mivel az origón áthaladó görbék által
bezárt szögek a leképezésnél megháromszorozódnak.
13. hét: Komplex
függvények integrálása
Komplex vonalintegrál.
Cauchy formula. Reziduum tétel.
1. Bevezetés. A komplex függvények előző
heti vizsgálatánál már utaltunk arra, hogy módszereink alapjául az egyváltozós
valós analízis illetve a síkbeli vektormezők elmélete szolgálnak. Ezen analógia
formálisan a komplex függvény értéke ![]() közvetlenül z -függvényében
való vizsgálatát, illetve a valós és képzetes részből kiindulva ( mivel
közvetlenül z -függvényében
való vizsgálatát, illetve a valós és képzetes részből kiindulva ( mivel ![]() ) az így kapott
) az így kapott ![]() síkbeli vektormező
használatát jelenti. E részben a komplex
integrálszámítással foglalkozunk. Egy "általános" (nem
okvetlenül differenciálható) komplex függvény integrálja kiszámításának módja
lényegében megfelel a vektormező vonalintegráljának, míg a deriválható komplex
függvények a potenciálos vektormezők elméletéhez hasonló tulajdonságokkal
rendelkeznek.
síkbeli vektormező
használatát jelenti. E részben a komplex
integrálszámítással foglalkozunk. Egy "általános" (nem
okvetlenül differenciálható) komplex függvény integrálja kiszámításának módja
lényegében megfelel a vektormező vonalintegráljának, míg a deriválható komplex
függvények a potenciálos vektormezők elméletéhez hasonló tulajdonságokkal
rendelkeznek.
2 Komplex függvény vonalintegrálja. Ezen integrálfogalom bevezetése új gondolatokat nem tartalmaz, alapulhat a szokásos technikán (részletösszegek határértéke). Ezt itt most nem ismételjük meg, helyette (kicsit erősebb feltételek mellett) rögtön egy számításra alkalmas alakú megfogalmazást közlünk.
1. Definíció (komplex vonalintegrál).
Tekintsük az ![]() folytonos komplex függvényt a
D
nyílt tartományon. Legyen G egy
reguláris síkgörbe a D -ben
(azaz
folytonos komplex függvényt a
D
nyílt tartományon. Legyen G egy
reguláris síkgörbe a D -ben
(azaz ![]() ). Akkor az f függvény G görbe mentén vett vonalmenti integrálja alatt az alábbi
kifejezésekkel meghatározott komplex számot értjük (közöljük a komplex
illetőleg a valós, képzetes részes alakot is):
). Akkor az f függvény G görbe mentén vett vonalmenti integrálja alatt az alábbi
kifejezésekkel meghatározott komplex számot értjük (közöljük a komplex
illetőleg a valós, képzetes részes alakot is): 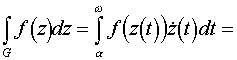
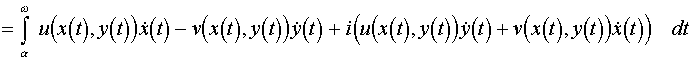 .
.
Megjegyezzük, hogy az imént definiált komplex integrál rendelkezik a szokásos integrál tulajdonságokkal (lineáris, additív stb.).
1. Tétel. (Cauchy-tétel.) Ha az ![]() függvény analitikus a D egyszeresen összefüggő nyílt tartományban és G egy zárt
reguláris síkgörbe a D -ben,
akkor
függvény analitikus a D egyszeresen összefüggő nyílt tartományban és G egy zárt
reguláris síkgörbe a D -ben,
akkor ![]() .
.
2. Definíció (primitív függvény). Legyen
az ![]() komplex függvény
megadott a D nyílt tartományon. Ha létezik egy
komplex függvény
megadott a D nyílt tartományon. Ha létezik egy ![]() deriválható komplex
függvény, melyre
deriválható komplex
függvény, melyre ![]() , akkor ezt az F függvényt a f függvény primitív
függvényének nevezzük a D tartományon.
, akkor ezt az F függvényt a f függvény primitív
függvényének nevezzük a D tartományon.
2. Tétel. Az ![]() (D egyszeresen összefüggő nyílt tartomány) analitikus függvénynek létezik primitív függvénye.
(D egyszeresen összefüggő nyílt tartomány) analitikus függvénynek létezik primitív függvénye.
Megjegyzés. Az előbbi Cauchy-tétel (1. tétel), amit szoktak a komplex függvénytan főtételének is nevezni, közvetlen következménye, hogy deriválható (analitikus) komplex függvények vonalintegrálja nem függ az úttól, csak annak végpontjaitól. A 2. tétel más szavakkal azt jelenti, hogy érvényben marad a Newton-Leibniz formula:
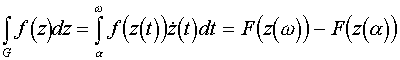 .
.
3. Cauchy formula. Reziduum tétel. Ebben a pontban közlünk két nagy elméleti jelentőségű tételt, melyek izolált szingularitások kivételével differenciálható komplex függvények vonalintegrálja számításánál alkalmazhatók.
3. tétel. (Cauchy integrálformula)
Legyen ![]() függvény analitikus, G pozitív körüljárású egyszerű zárt görbe, mely belsejével együtt
a D tartományban fekszik és a z pontot belsejében tartalmazza.
Akkor
függvény analitikus, G pozitív körüljárású egyszerű zárt görbe, mely belsejével együtt
a D tartományban fekszik és a z pontot belsejében tartalmazza.
Akkor 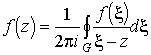 .
.
4. tétel. (Laurent sor) Legyen az ![]() függvény analitikus
(vagyis az f a D nyílt tartományon egy szinguláris pont
kivételével mindenütt analitikus). Akkor az
f
függvény a szinguláris pont környezetében un. Laurent sorba fejthető:
függvény analitikus
(vagyis az f a D nyílt tartományon egy szinguláris pont
kivételével mindenütt analitikus). Akkor az
f
függvény a szinguláris pont környezetében un. Laurent sorba fejthető: 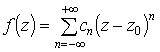 .
.
5. Tétel. (reziduum tétel) Legyen f függvény analitikus
a G
pozitív körüljárású egyszerű zárt görbén, illetve annak belsejében véges
sok izolált szinguláris pont ![]() kivételével.
Jelöljük
kivételével.
Jelöljük ![]() -vel az f függvény
-vel az f függvény ![]() -beli Laurent sora
-beli Laurent sora ![]() együtthatóját.
Akkor
együtthatóját.
Akkor ![]() .
.
14. hét: Parciális differenciálegyenletek
Parciális differenciálegyenletek. Problémafelvetés, osztályozás, utalás
a főbb megoldási módszerekre. A Fourier módszer. A hővezetés
differenciálegyenlete.
Kurzusunkban nincs lehetőség a parciális differenciálegyenletek részletes tárgyalására. A foglalkozáson emlékeztetünk a főbb fogalmakra (egyenlet, kezdeti, peremfeltételek stb). Néhány példán szemléltetjük, hogyan vezethető vissza a probléma már tárgyalt kérdésekre, elsősorban közönséges egyenletekre.
15. hét: Laplace
transzformáció
A Laplace transzformáció. Elemi
függvények, eltolás, derivált, integrál Laplace transzformáltja. Alkalmazás
differenciál és integrálegyenletekre.
A Laplace transzformáció az alkalmazott matematika egyik fontos módszere a mérnöki gyakorlatban (pl. szabályozáselmélet). Hatásának lényege összefoglal-ható abban , hogy a differenciálás és integrálás műveletét visszavezeti a független változóval való szorzás illetve osztásra, bizonyos differenciál- illetve integrálegyenletek megoldását algebrai egyenletek megoldására.
1. Definíció (Laplace transzformált).
Legyen: ![]() -ra, ha az
-ra, ha az 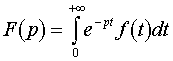 improprius integrál
konvergens, akkor az F függvényt a
f függvény Laplace
transzformáltjának nevezzük.
improprius integrál
konvergens, akkor az F függvényt a
f függvény Laplace
transzformáltjának nevezzük.
(A Laplace
transzformáltra az ![]() jelöléseket
használjuk. Az F függvény p argumentuma általában véve komplex szám,
jelöléseket
használjuk. Az F függvény p argumentuma általában véve komplex szám,
![]() ).
).
2. Laplace transzformálhatóság elégséges feltételei. (L1-2.)
(L1) f szakaszonként
folytonos a [0,![]() ) intervallumon,
) intervallumon,
(L2) ![]() melyekre
melyekre ![]()
![]() esetén.
esetén.
Megjegyzés: ![]() -re az előbbi feltételek mellett a Laplace transzformáltat
definiáló improprius integrál értelmezhető és konvergens.
-re az előbbi feltételek mellett a Laplace transzformáltat
definiáló improprius integrál értelmezhető és konvergens.
3.
Laplace transzformált ![]() -nél.
-nél.
Állítás: Ha f kielégíti az (L) feltételeket, akkor ![]() .
.
(Megjegyzés. A
racionális törtfüggvény alakú Laplace transzformáltak számlálójának fokszáma
mindig kisebb a nevező fokszámánál.)
4.Néhány
elemi függvény Laplace transzformáltja.
Heaviside függvény (egységugrás) ![]() . A Laplace transzformált adódik a definiáló improprius
integrál kiszámításával (konvergencia
. A Laplace transzformált adódik a definiáló improprius
integrál kiszámításával (konvergencia ![]() -ra), azaz
-ra), azaz 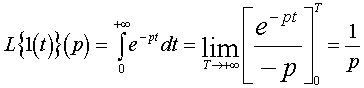 .
.
![]() . A definícióból hasonlóan
. A definícióból hasonlóan
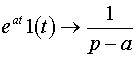 (p>a).
(p>a).
5. A Laplace operátor elemi tulajdonságai.
Az alábbiakban felsorolt tulajdonságok bizonyításai elemi úton adódnak közvetlenül a definícióból. A konvergenciára illetve a függvényekre vonatkozó pontos feltételek megfogalmazásától időnként eltekintünk, ls.[ ]. Az itt felsoroltakat nehány elemi függvény Laplace transzformáltjával együtt egy összefoglaló táblázatban később közöljük.
a).
Lineáris operator. Ha f,
g függvények kielégítik az (L) feltételeket ![]() állandókkal és
állandókkal és ![]()
![]() (
(![]() ).
).
b). Eltolások.
Eltolás p- ben ![]() .
.
Eltolás t- ben ![]() .
.
c). Periodikus függvény Laplace transzformáltja.
Ha ![]() , akkor
, akkor 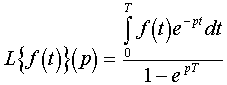 .
.
6. Deriválás, integrálás.
a). Laplace transzformált deriváltja. ![]() .
.
b). Derivált Laplace transzformáltja. ![]() .
.
Az utóbbi két tulajdonság általánosítható az n. derivált esetére (ls. 15.1 táblázat).
c). Integrál
Laplace transzformáltja. 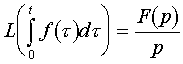 .
.
d). Konvolúciós integrál Laplace transzformáltja ![]() .
.
Itt 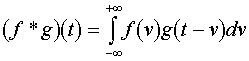 .
.
7. Összefoglaló táblázat.
|
f |
F |
|
f |
F |
|
1(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin at |
|
|
|
|
|
cos at |
|
|
|
|
|
sh at |
|
|
|
|
|
ch at |
|
|
|
|
8. A Laplace transzformáció alkalmazásai.
Kidolgozott példák.
8.1. példa. Keressük meg az ![]() állandó-együtthatós
inhomogén lineáris differenciálegyenlet
állandó-együtthatós
inhomogén lineáris differenciálegyenlet
![]() kezdeti érték feladatának
megoldását.
kezdeti érték feladatának
megoldását.
Megoldás (8.1. példa).
Vegyük az egyenlet mindkét oldalának Laplace transzformáltját (eközben kihasználjuk a bal oldalon a Laplace transzformált linearitását, a derivált transzformáltjára vonatkozó összefüggést, a jobb oldalon az x elemi függvény Laplace traszformáltját illetve az eltolási tételt.)
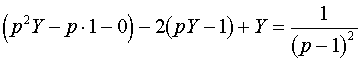 .
.
A kifejezést Y-ra rendezve, a kapott törtet parciális törtekre bontva megkapjuk az eredmény Laplace transzformáltját
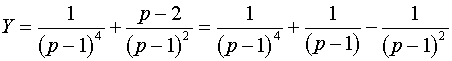 .
.
Ebből az
alakból már könnyen adódik (a 8. táblázat összefüggéseiből) a keresett megoldás
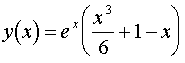 .
.
8.2. példa.
Oldjuk meg az 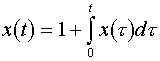 integrálegyenletet.
(Megjegyezzük, hogy ezen egyenlet ekvivalens /ls. 2. hét/ az
integrálegyenletet.
(Megjegyezzük, hogy ezen egyenlet ekvivalens /ls. 2. hét/ az ![]() differenciálegyenlettel.)
differenciálegyenlettel.)
Megoldás
(8.2. példa). Hasonlóan az előző feladathoz mindkét oldal Laplace transzformáltját véve 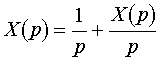 adódik. Innen
adódik. Innen ![]() , azaz
, azaz
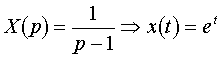 .
.